Bán kính đường tròn ngoại tiếp tam giác là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn lớp 9 tham khảo.
Cách tính bán kính đường tròn ngoại tiếp tam giác tổng hợp toàn bộ kiến thức lý thuyết, công thức tính, ví dụ minh họa và các dạng bài tập tính bán kính đường tròn ngoại tiếp tam giác. Qua tài liệu này các em có thêm nhiều tư liệu ôn tập, trau dồi kiến thức để nhanh chóng giải được các bài tập Toán 9. Từ đó đạt được kết quả cao trong các bài kiểm tra, bài thi vào lớp 10 môn Toán. Vậy sau đây là nội dung chi tiết Cách tính bán kính đường tròn ngoại tiếp tam giác, mời các bạn cùng theo dõi và tải tài liệu tại đây.
1. Công thức tính bán kính đường tròn ngoại tiếp
Cho tam giác ABC có AB = c, AC = b, BC = a, R là bán kính đường tròn ngoại tiếp tam giác ABC, S là diện tích tam giác ABC
Cách 1: Sử dụng công thức diện tích tam giác
Cách 2: Sử dụng định lí Sin trong tam giác
Ta có:
Cách 3: Tính chất của tam giác vuông
– Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền, do đó bán kính đường tròn ngoại tiếp tam giác vuông chính bằng nửa độ dài cạnh huyền.
Cách 4: Sử dụng hệ tọa độ
– Tìm tọa độ tâm O của đường tròn ngoại tiếp tam giác ABC
– Tìm tọa độ một trong ba đỉnh A, B, C (nếu chưa có)
– Tính khoảng cách từ tâm O tới một trong ba đỉnh A, B, C, đây chính là bán kính cần tìm: R = OA = OB = OC
2. Ví dụ tính bán kính đường tròn ngoại tiếp tam giác
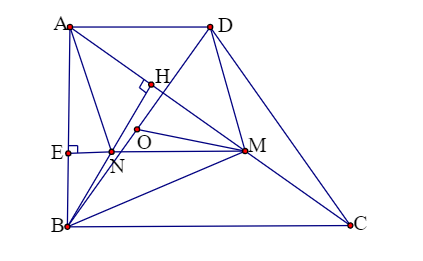
Ví dụ 1: Cho hình thang vuông ABCD có , BC = 2AD = 2a. Gọi H là hình chiếu vuông góc của B lên AC, M là trung điểm của HC. Tìm tâm và bán kính của đường tròn ngoại tiếp tam giác BDM.
Gợi ý trả lời
Vẽ hình:
Gọi N là trung điểm của BH thì MN là đường trung bình của tam giác HBC => MN ⊥ AB
Mặt khác BH ⊥ AM
=> N là trực tâm của tam giác ABM
=> AN ⊥ BM
Do => MN //= AD
Nên ADMN là hình bình hành => AN // DM
Từ đó ta có: DM ⊥ MB hay tam giác DBM vuông tại M nên tâm đường tròn ngoại tiếp tam giác DBM là trung điểm O của BD
Ta có:
Ví dụ 2: Cho tam giác ABC có AB = 3, AC = 5 và BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Gợi ý đáp án
Theo công thức Hê – rông, diện tích tam giác A B C là:
Bán kính đường tròn ngoại tiếp tam giác ABC là:
3. Bài tập tính bán kính đường tròn ngoại tiếp tam giác
Bài 1: Cho tam giác ABC vuông tại A có AB = 1; AC = 4. Gọi M là trung điểm AC.
a) Tính diện tích tam giác ABC.
b) Tính bán kính R1 của đường tròn ngoại tiếp tam giác ABC.
c) Tính bán kính R2 của đường tròn ngoại tiếp tam giác CBM.
Bài 2: Cho tam giác ABC có BC = 10. Gọi (I) là đường tròn có tâm I thuộc cạnh BC và tiếp xúc với các cạnh AB, AC lần lượt tại M và N. Biết đường tròn (I) có bán kính bằng 3 và 2IB = 3IC. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
Bài 3: Cho tam giác ABC vuông tại A, Ab = 5cm, AC = 12cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Bài 4: Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Chứng minh rằng 4 điểm A, B, C, D cùng nằm trên một đường tròn. Tính bán kính đường tròn đó.
Bài 5: Cho hình vuông ACBD. Gọi M, N lần lượt là trung điểm của AB và BC. Gọi E là giao điểm của AM và DN
a) Tính số đo góc CEN
b) Chứng minh 4 điểm A, D, E, M thuộc cùng 1 đường tròn.
c) Xác định tâm đường tròn ngoại tiếp đi qua ba điểm B, D, E,.
Bài 6; Cho tam giác ABC có AB = 3, AC = 5 và BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
