Giải bài toán bằng cách lập phương trình là dạng bài tập tương đối phổ biến ở bậc THCS. Để các bạn học sinh có thể hiểu rõ và vận dụng làm các bài Toán tốt hơn. HOCMAI đã tổng hợp các phương pháp, các dạng bài giải bằng cách lập phương trình theo cấp độ từ cơ bản đến nâng cao trong bài viết này.
I. Lý thuyết quan trọng cần nhớ
1. Các bước để giải bài toán bằng cách lập phương trình
Để làm được dạng bài giải bài toán bằng cách lập phương trình, các bạn học sinh cần thực hiện theo các bước dưới đây:
Bước 1: Lập phương trình
Sẽ có 4 công việc các bạn cần làm trong bước này:
- Xác định đại lượng bài cần tìm, đại lượng đã cho và mối quan hệ giữa các đại lượng.
- Chọn ẩn phù hợp và đặt điều kiện cho ẩn số.
- Biểu diễn các đại lượng đã và chưa biết theo ẩn.
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình đã lập ở bước 1
Bước 3: Kiểm tra lại nghiệm phương trình và kết luận
Có tất cả 2 công việc bạn phải làm trong bước này:
- Kiểm tra xem có nghiệm nào thỏa mãn điều kiện của ẩn không?
- Trả lời câu hỏi ở đề bài.
2. Các lưu ý về việc chọn ẩn và điều kiện thích hợp của ẩn:
Có 4 lưu ý khi thực hiện việc việc chọn ẩn và điều kiện thích hợp của ẩn. Bao gồm:
+ Thông thường sẽ chọn ẩn là đại lượng có trong câu hỏi.
+ Nếu biểu thị của x là một chữ số => 0 ≤ x ≤ 9
+ x sẽ mang giá trị nguyên dương nếu biểu thị cho tuổi, sản phẩm, người,..
+ x > 0 nếu x biểu thị vận tốc chuyển động.
II. Các dạng bài giải bằng cách lập phương trình (Có ví dụ đi kèm)
Để dễ dàng trong việc xác định các đại lượng có trong bài cũng như biểu diễn mối quan hệ giữa các đại lượng đó. Chúng ta có 4 dạng cơ bản giải bài toán bằng cách lập phương trình.
Dạng 1: Dạng bài toán về chuyển động
Kiến thức quan trọng cần nhớ về bài toán chuyển động:
A. Có 3 đại lượng chính trong bài toán về chuyển động:
- Quãng đường – Ký hiệu là S
- Thời gian – Ký hiệu là t
- Vận tốc – Ký hiệu là v
B. Công thức liên hệ của 3 đại lượng:
- S = t.v | Quãng đường = Vận tốc x Thời gian.
- v= S/t | Vận tốc = Quãng đường / Thời gian.
- t = S/v | Thời gian = Quãng đường /Vận tốc.
C. 3 đại lượng phải có đơn vị tương ứng với nhau:
Ví dụ: S là km => v là km/h và t là km/h.
Ví dụ: Có một xe khách đi từ điểm A đến điểm B với v = 50 km/h, sau khi trả khách thì đi từ B về A với v = 40 km/h. Tổng thời gian cả đi và về hết 5 giờ 24 phút. Tìm S từ A đến B?
Lời giải:
Dạng 2: Dạng toán về năng suất
Kiến thức cần nhớ về bài toán năng suất:
A. Có 3 đại lượng chính trong bài toán về chuyển động:
- Năng suất làm việc là N
- Thời gian hoàn thành công việc là t
- Khối lượng công việc là CV
B. Công thức liên hệ giữa 3 đại lượng:
- CV = N x t | K.lượng công việc = Năng suất x Thời gian.
- N = CV/t | Năng suất = K.lượng công việc / Thời gian.
- t = CV/N | K.lượng công việc / Năng suất.
C. Dạng bài tập về năng suất cần chú ý:
Bài toán về hoàn thành chung hay riêng về một công việc; vòi nước chảy chung hay riêng. Lúc này ta coi toàn bộ công việc là 1 đơn vị để giải.
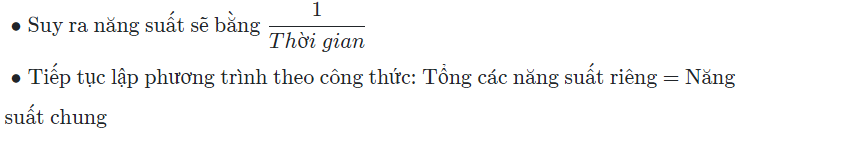
Ví dụ: Hai đội thợ phải hoàn thành việc quét sơn trong một văn phòng. Nếu làm đơn lẻ thì đội I hoàn thành công việc nhanh hơn đội II thời gian là 6 ngày. Còn nếu họ cùng làm thì chỉ cần 4 ngày để hoàn thành công việc. Hỏi nếu các đội làm việc đơn lẻ thì thời gian hoàn thành công việc của mỗi đội là bao lâu?
Lời giải

Dạng 3: Dạng toán về số và chữ số
Kiến thức quan trọng cần nhớ:
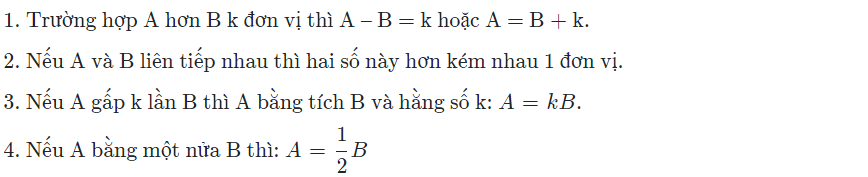
Ví dụ: Tìm một số tự nhiên có hai chữ số, gợi ý:
- Chữ số hàng chục và chữ số hàng đơn vị có hiệu là -2
- Tích hai số này là 15
Lời giải

Dạng 4: Dạng toán về hình học
Kiến thức quan trọng cần nhớ:
- Diện tích tam giác vuông = tích hai cạnh góc vuông chia 2.
- Diện tích hình chữ nhật = chiều dài x chiều rộng.
- Diện tích hình vuông = cạnh x cạnh.
Ví dụ: Ông A có một mảnh đất hình chữ nhật có S = 320m2, chiều rộng bé < chiều dài 4 mét. Tìm ra CD và CR mảnh đất này.
Lời giải

Bài tập ôn luyện từ cơ bản đến nâng cao dạng toán Giải bài toán bằng cách lập phương trình:
Trên đây là toàn bộ kiến thức về giải bài toán bằng cách lập hệ phương trình. Hy vọng đây sẽ là những kiến thức bổ ích giúp các em học sinh trong quá trình làm bài tập Toán lớp 9 cũng như trong quá trình ôn thi vào 10 môn Toán.

