Tam giác đồng dạng là gì ? Cách chứng minh hai tam giác đồng dạng
Chuyên đề về tam giác đồng dạng cũng như cách chứng minh hai tam giác đồng dạng học sinh đã được tìm hiểu trong chương trình Toán 8, phân môn Hình học. Đây là phần kiến thức vô cùng quan trọng của chương trình. Bài viết hôm nay, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá sẽ hệ thống lại tất cả các kiến thức cần ghi nhớ về chuyên đề này. Bạn tìm hiểu nhé !
I. LÝ THUYẾT VỀ TAM GIÁC ĐỒNG DẠNG
Bạn đang xem bài: Tam giác đồng dạng là gì ? Cách chứng minh hai tam giác đồng dạng
1. Định nghĩa hai tam giác đồng dạng
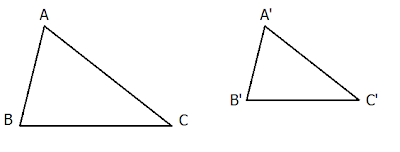
Hai tam giác đồng dạng là gì? “Đồng dạng” là từ Hán Việt và vốn có nghĩa là giống nhau. Hai tam giác đồng dạng với nhau khi chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Tam giác ABC và tam giác A’B’C’ được gọi là đồng dạng với nhau nếu: A^=A′^;B^=B′^;C^=C′^
và A′B′AB=B′C′BC=A′C′AC
Kí hiệu hai tam giác đồng dạng: △ABC∼△A′B′C′
Tỉ số: A′B′AB=B′C′BC=A′C′AC=k được gọi là tỉ số đồng dạng.
2. Các trường hợp đồng dạng của tam giác thường
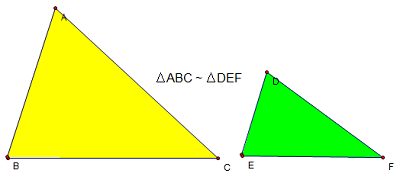
- Trường hợp 1: Ba cạnh tương ứng tỉ lệ nhau (c – c – c).
Xét hai tam giác ABC và DEF có:
ABDE=ACDF=BCEF
Suy ra: △ABC∼△DEF (c – c – c)
- Trường hợp 2: Hai cạnh tương ứng tỉ lệ nhau – góc xen giữa hai cạnh bằng nhau (c – g – c).
Xét hai tam giác ABC và DEF, ta có:
ABDE=ACDF
A^=D^
Suy ra: △ABC∼△DEF (c – g – c)
- Trường hợp 3: Hai góc tương ứng bằng nhau (g – g)
Xét hai tam giác ABC và DEF có:
A^=D^
B^=E^
Suy ra: △ABC∼△DEF (g – g)
3. Các định lý đồng dạng của tam giác vuông
- Định lý 1: Cạnh huyền – Cạnh góc vuông
Nếu cạnh huyền và cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác đó đồng dạng.
- Định lý 2: Hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác đó đồng dạng.
- Định lý 3: Góc của hai tam giác vuông
Nếu góc nhọn của tam giác vuông này bằng góc nhọn của tam giác vuông kia thì hai tam giác đó đồng dạng.
II. CÁCH CHỨNG MINH HAI TAM GIÁC ĐỒNG DẠNG
Dạng 1 : Chứng minh hai tam giác đồng dạng – Hệ thức :
Bài toán: Cho △ABC(AB<AC), AD là đường phân giác trong. Miền ngoài △ vẽ tia Cx sao cho BCxˆ=BADˆ. Gọi I là giao điểm của Cx và AD. Chứng minh rằng:
- a) △ADB∼△CDI
- b) ADAC=ABAI
- c) AD2 = AB.AC – BD.DC
Cách giải:
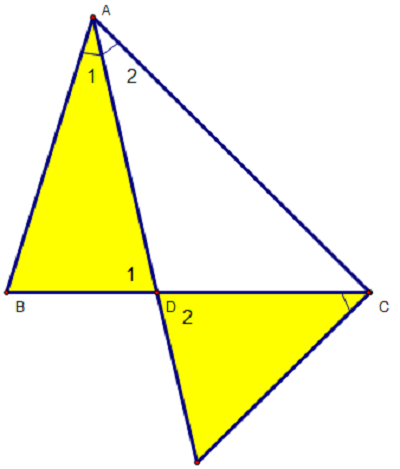
a) Xét △ADB và △CDI , ta có:
BCxˆ=BADˆ (gt)
D1ˆ=D2ˆ (đối đỉnh)
Suy ra: △ADB∼△CDI
b) Xét △ABD và △AIC , ta có :
Bˆ=Iˆ (△ADB∼△CDI)
A1ˆ=A2ˆ(AD là phân giác)
Suy ra △ABD∼△AIC
Suy ra ADAC=ABAI, suy ra AD.AI = AB.AC (1)
c) Có ADCD=BDBI △ADB∼△CDI
Suy ra: AD.DI = BD.CD (2)
từ (1) và (2) :
Suy ra: AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI ) = AD.AD = AD2
Dạng 2: Chứng minh hai tam giác đồng dạng – Định lí Talet và Hai đường thẳng song song
Bài toán:
Cho tam giác ABC nhọn, đường cao BD và CE. Kẻ các đường cao DF và EG của tam giác ADE. Chứng minh:
- a) △ADB∼△AEG
- b) AD.AE = AB.AG = AC.AF
- c) FG // BC
Cách giải:
a) Xét tam giác ABD và AEG, ta có :
BD AC (BD là đường cao)
EG AC (EG là đường cao)
Suy ra: BD // EG
Suy ra: △ADB∼△AEG
b) Từ a) Suy raABAE=ADAG
⇒ AD.AE = AB.AG (1)
CM tương tự, ta được : AD.AE = AC.AF (2)
Từ (1) và (2) suy ra :
AD.AE = AB.AG = AC.AF
c) Xét tam giác ABC, ta có :
AB.AG = AC.AF (cmb) suy ra: ABAF=ACAG
Suy ra: FG // BC (định lí Talet đảo)
Dạng 3: Chứng minh hai tam giác đồng dạng – góc tương ứng bằng nhau
Bài toán: Cho tam giác ABC có các đường cao BD và CE cắt nhau tại H. Chứng minh:
- a) Tam giác HBE và tam giác HCE đồng dạng.
- b) △HED∼△HBC
và HDEˆ=HAEˆ
Cách giải:

a) Xét tam giác HBE và tam giác HCD, ta có :
BEHˆ=CDHˆ=90∘ (gt)
H1ˆ=H2ˆ (đối đỉnh)
Suy ra: △HBE∼△HCD (g – g)
b) Xét tam giác HED và HBC, ta có :
HEHD=HDHC (△HBE∼△HCD)
Suy ra: HEHD=HDHC
EHDˆ=CHBˆ(đối đỉnh)
Suy ra △HED∼△HBC(c – g – c)
Suy ra: D1ˆ=C1ˆ(1)
mà còn có: đường cao BD và CE cắt nhau tại H (gt)
III. BÀI TẬP CHỨNG MINH HAI TAM GIÁC ĐỒNG DẠNG
1. Bài tập có lời giải:
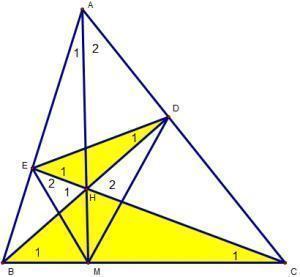
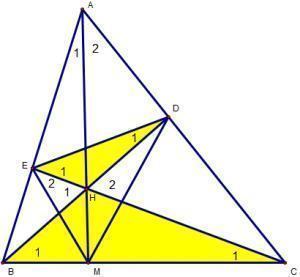
Bài 1: Cho ∆ABC có các đường cao BD và CE cắt nhau tại H. Chứng minh :
a) ∆HBE đồng dạng ∆HCE.
b) ∆HED đồng dạng ∆HBC và 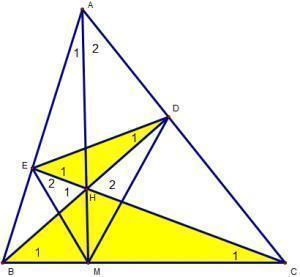
c) cho biết BD = CD. Gọi M là giao điểm của AH và BC. chứng minh : DE vuông góc EM.
Giải
 a) xét ∆HBE và ∆HCD, ta có :
a) xét ∆HBE và ∆HCD, ta có :
 (gt)
(gt)
 (đối đỉnh)
(đối đỉnh)
=> ∆HBE ~ ∆HCD (g – g)
b) ∆HED và ∆HBC, ta có :
 (∆HBE ~ ∆HCD)
(∆HBE ~ ∆HCD)
=> 
 (đối đỉnh)
(đối đỉnh)
=> ∆HED ~ ∆HBC (c – g – c)
=>  (1)
(1)
mà : Đường cao BD và CE cắt nhau tại H (gt)
=> H là trực tâm.
=> AH ⊥ BC tại M.
=> 
mặt khác: 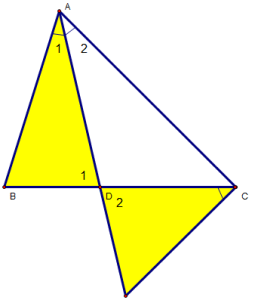
=>  (2)
(2)
từ (1) và (2) : 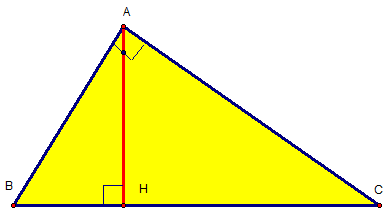
hay: 
c) cmtt câu b, ta được: (3)
xét ∆BCD, ta có :
DB = DC (gt)
=> ∆BCD cân tại D
=>
mà: (∆HED ~ ∆HBC)
=>
mà:
(cmt)
=>
hay:
=> ED ⊥ EM.
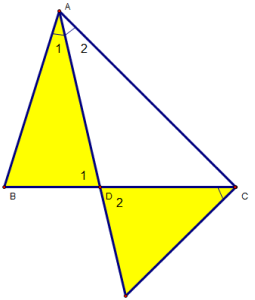
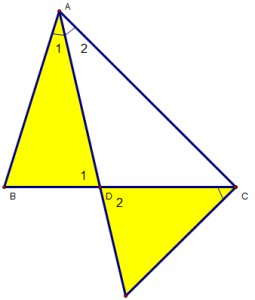
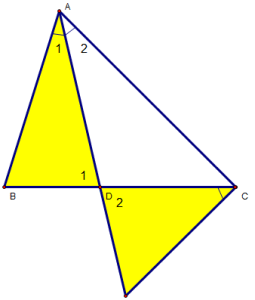
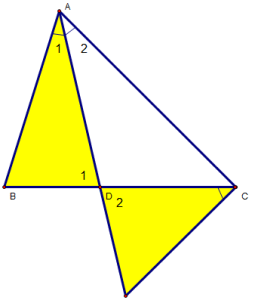
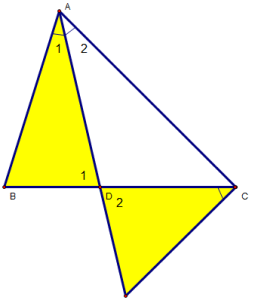
Bài 2: Cho ∆ABC (AB < AC), có AD là đường phân giác trong. Ở miền ngoài ∆ABC vẽ tia Cx sao cho . Gọi I là giao điểm của Cx và AD. cmr :
a) ∆ADB đồng dạng ∆CDI.
b)
c) AD2 = AB.AC – BD.DC
Giải
a) ∆ADB và ∆CDI , ta có : (gt)
(đối đỉnh)
=> ∆ADB ~ ∆CDI
b) ∆ABD và ∆AIC , ta có : (∆ADB ~ ∆CDI)
(AD là phân giác)
=> ∆ABD ~ ∆AIC
=>
c) => AD.AI = AB.AC (1)
mà : (∆ADB ~ ∆CDI )
=> AD.DI = BD.CD (2)
từ (1) và (2) :AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI ) = AD.AD = AD2
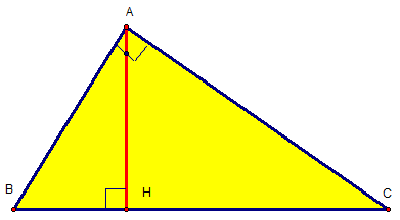
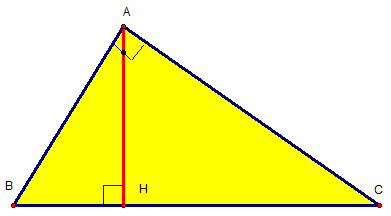
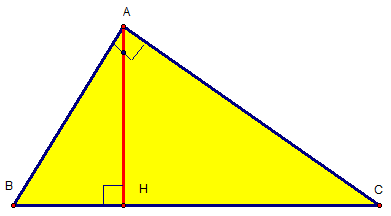
Bài 3: Cho tam giác ABC vuông tại A, có đường cao AH . Chứng minh các hệ thức :
a. AB2 = BH.BC và AC2 = CH.BC
b. AB2 +AC2 = BC2
c. AH2 = BH.CH
d. AH.BC = AB.AC
Giải.
Xét hai ∆ABC và ∆ HAC, ta có:
a. AC2 = CH.BC :
là góc chung.
=> ∆ABC ~ ∆HAC (g – g)
=>
=> AC2 = CH.BC (1)
Cmtt : AB2 = BH.BC (2)
b. AB2 +AC2 = BC2
Từ (1) và (2), ta có :
AB2 +AC2 = BH.BC + CH.BC = (BH + CH)BC = BC2
c. AH2 = BH.CH :
Xét hai ∆HBA và ∆ HAC, ta có :
cùng phụ
=> ∆HBA ~ ∆HAC (g – g)
=>
=> AH2 = BH.CH
d. AH.BC = AB.AC :
Ta có : (∆ABC ~ ∆HAC)=> AH.BC = AB.AC.
Bài 4: Cho ∆ABC nhọn. kẻ đường cao BD và CE. vẽ các đường cao DF và EG của ∆ADE. Chứng minh
a) ∆ABD đồng dạng ∆AEG.
b) AD.AE = AB.AG = AC.AF
c) FG // BC
Giải
a) xét ∆ABD và ∆AEG, ta có :BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
=> BD // EG
=> ∆ABD ~ ∆AGE
b) =>
=> AD.AE = AB.AG (1)
cmtt, ta được : AD.AE = AC.AF (2)
từ (1) và (2) suy ra :AD.AE = AB.AG = AC.AF
c) xét ∆ABC, ta có :AB.AG = AC.AF (cmt)
=> FG // BC (định lí đảo talet)
Do đó H là trực tâm, suy ra AH⊥BC tại M.
Suy raA1ˆ+ABCˆ=90∘
Mặt khác : C1ˆ+ABCˆ=90∘
Suy ra: A1ˆ=C1ˆ (2)
Từ (1) và (2) => A1ˆ=D1ˆ
hay: HDEˆ=HAEˆ
2. Bài tập tự luyện thêm
Bài 1: Cho tam giác ABC vuông tại A , đường cao AH. Chứng minh:
a/ AH.BC = AB.AC
b/ AB² = BH.BC
c/ AH² = BH.CH
d/ Gọi M là trung điểm của BH, N là trung điểm của AH. Chứng minh: CN AM.
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền thành 2 đoạn BH = 9cm và HC = 16cm. Tính AB, AC, BC.
Bài 3: Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 21cm; AC = 28cm.
a/ Tính AH
b/ Kẻ HD AB; HE AC. Tính diện tích tam giác AED.
Bài 4: Cho tam giác ABC vuông tại A có AB = 15cm, AC = 20cm. Kẻ đường cao AH, trung tuyến AM.
a/ Tính AH; BC. b/ Tính BH,CH. c/ Tính diện tích tam giác AHM.
Bài 5: Cho có ba góc nhọn, đường cao AH. Vẽ HD vuông góc AB tại D, HE vuông góc AC tại E.
a) Chứng minh: tam giác AHB đồng dạng với tam giác ADH và tam giác AHC đồng dạng với tam giác AEH.
b) Chứng minh: AD.AB = AE.AC.
c) Cho AB = 12 cm, AC = 15 cm, BC = 18 cm. Tính độ dài đường phân giác AK của (K thuộc BC)
Bài 6: Cho ABC có AB = 3 cm, AC = 4 cm, BC = 5 cm. Đường phân giác góc A cắt cạnh BC tại D. Qua D vẽ đường thẳng vuông góc với BC cắt AC tại E và BA tại K.
a/ Chứng minh ABC vuông
b/ Tính DB, DC
c/ Chứng minh tam giác EDC đồng dạng với tam giác BDK
d/ Chứng minh DE = DB
Bài 7: Cho ABC vuông tại A, cho biết AB = 15 cm, AC = 20 cm. Kẻ đường cao AH của ABC.
a) Chứng minh: tam giác AHB đồng dạng với tam giác CAB và suy ra AB² = BH.BC
b) Tính độ dài các đoạn thẳng BH và CH.
c) Kẻ HM vuông góc với AB và HN vuông góc với AC. Chứng minh: AM.AB = AN.AC
d)Chứng minh: tam giác AMN đồng dạng với tam giác ACB
Bài 8: Cho tam giác ABC vuông tại A. Đường phân giác của góc A cắt cạnh huyền BC tại D. Qua D kẻ đường thẳng vuông góc với BC và cắt AC tại E.
a) Chứng minh tam giác DEC đồng dạng với tam giác ABC.
b) Chứng minh: DB = DE.
Bài 9: Cho tam giác ABC vuông tại A có AB = 16cm, BC = 20cm. Kẻ đường phân giác BD (D thuộc AC)
a) Tính CD và AD
b) Từ C kẻ CH vuông góc với BD tại H. Chứng minh: Tam giác ABD đồng dạng với tam giác HCD
c) Tính diện tích tam giác HCD .
Trên đây, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá.vn đã giới thiệu đến quý thầy cô và các bạn tam giác đồng dạng là gì ? Cách chứng minh hai tam giác đồng dạng nhanh nhất. Hi vọng, bài viết đã cung cấp cho bạn những thông tin hữu ích. Xem thêm cách chứng minh hình thang tại đường link này nhé !
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận! Nguồn chia sẻ: https://tmdl.edu.vn/tam-giac-dong-dang-la-gi-cach-chung-minh-hai-tam-giac-dong-dang/
Tam giác đồng dạng là gì ? Cách chứng minh hai tam giác đồng dạng
Chuyên đề về tam giác đồng dạng cũng như cách chứng minh hai tam giác đồng dạng học sinh đã được tìm hiểu trong chương trình Toán 8, phân môn Hình học. Đây là phần kiến thức vô cùng quan trọng của chương trình. Bài viết hôm nay, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá sẽ hệ thống lại tất cả các kiến thức cần ghi nhớ về chuyên đề này. Bạn tìm hiểu nhé !
I. LÝ THUYẾT VỀ TAM GIÁC ĐỒNG DẠNG
Bạn đang xem bài: Tam giác đồng dạng là gì ? Cách chứng minh hai tam giác đồng dạng
1. Định nghĩa hai tam giác đồng dạng
Hai tam giác đồng dạng là gì? “Đồng dạng” là từ Hán Việt và vốn có nghĩa là giống nhau. Hai tam giác đồng dạng với nhau khi chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Tam giác ABC và tam giác A’B’C’ được gọi là đồng dạng với nhau nếu: A^=A′^;B^=B′^;C^=C′^
và A′B′AB=B′C′BC=A′C′AC
Kí hiệu hai tam giác đồng dạng: △ABC∼△A′B′C′
Tỉ số: A′B′AB=B′C′BC=A′C′AC=k được gọi là tỉ số đồng dạng.

2. Các trường hợp đồng dạng của tam giác thường
- Trường hợp 1: Ba cạnh tương ứng tỉ lệ nhau (c – c – c).
Xét hai tam giác ABC và DEF có:
ABDE=ACDF=BCEF
Suy ra: △ABC∼△DEF (c – c – c)
- Trường hợp 2: Hai cạnh tương ứng tỉ lệ nhau – góc xen giữa hai cạnh bằng nhau (c – g – c).
Xét hai tam giác ABC và DEF, ta có:
ABDE=ACDF
A^=D^
Suy ra: △ABC∼△DEF (c – g – c)
- Trường hợp 3: Hai góc tương ứng bằng nhau (g – g)
Xét hai tam giác ABC và DEF có:
A^=D^
B^=E^
Suy ra: △ABC∼△DEF (g – g)

3. Các định lý đồng dạng của tam giác vuông
- Định lý 1: Cạnh huyền – Cạnh góc vuông
Nếu cạnh huyền và cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác đó đồng dạng.
- Định lý 2: Hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác đó đồng dạng.
- Định lý 3: Góc của hai tam giác vuông
Nếu góc nhọn của tam giác vuông này bằng góc nhọn của tam giác vuông kia thì hai tam giác đó đồng dạng.
II. CÁCH CHỨNG MINH HAI TAM GIÁC ĐỒNG DẠNG
Dạng 1 : Chứng minh hai tam giác đồng dạng – Hệ thức :
Bài toán: Cho △ABC(AB<AC), AD là đường phân giác trong. Miền ngoài △ vẽ tia Cx sao cho BCxˆ=BADˆ. Gọi I là giao điểm của Cx và AD. Chứng minh rằng:
- a) △ADB∼△CDI
- b) ADAC=ABAI
- c) AD2 = AB.AC – BD.DC
Cách giải:

a) Xét △ADB và △CDI , ta có:
BCxˆ=BADˆ (gt)
D1ˆ=D2ˆ (đối đỉnh)
Suy ra: △ADB∼△CDI
b) Xét △ABD và △AIC , ta có :
Bˆ=Iˆ (△ADB∼△CDI)
A1ˆ=A2ˆ(AD là phân giác)
Suy ra △ABD∼△AIC
Suy ra ADAC=ABAI, suy ra AD.AI = AB.AC (1)
c) Có ADCD=BDBI △ADB∼△CDI
Suy ra: AD.DI = BD.CD (2)
từ (1) và (2) :
Suy ra: AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI ) = AD.AD = AD2
Dạng 2: Chứng minh hai tam giác đồng dạng – Định lí Talet và Hai đường thẳng song song
Bài toán:
Cho tam giác ABC nhọn, đường cao BD và CE. Kẻ các đường cao DF và EG của tam giác ADE. Chứng minh:
- a) △ADB∼△AEG
- b) AD.AE = AB.AG = AC.AF
- c) FG // BC
Cách giải:

a) Xét tam giác ABD và AEG, ta có :
BD AC (BD là đường cao)
EG AC (EG là đường cao)
Suy ra: BD // EG
Suy ra: △ADB∼△AEG
b) Từ a) Suy raABAE=ADAG
⇒ AD.AE = AB.AG (1)
CM tương tự, ta được : AD.AE = AC.AF (2)
Từ (1) và (2) suy ra :
AD.AE = AB.AG = AC.AF
c) Xét tam giác ABC, ta có :
AB.AG = AC.AF (cmb) suy ra: ABAF=ACAG
Suy ra: FG // BC (định lí Talet đảo)
Dạng 3: Chứng minh hai tam giác đồng dạng – góc tương ứng bằng nhau
Bài toán: Cho tam giác ABC có các đường cao BD và CE cắt nhau tại H. Chứng minh:
- a) Tam giác HBE và tam giác HCE đồng dạng.
- b) △HED∼△HBC
và HDEˆ=HAEˆ
Cách giải:

a) Xét tam giác HBE và tam giác HCD, ta có :
BEHˆ=CDHˆ=90∘ (gt)
H1ˆ=H2ˆ (đối đỉnh)
Suy ra: △HBE∼△HCD (g – g)
b) Xét tam giác HED và HBC, ta có :
HEHD=HDHC (△HBE∼△HCD)
Suy ra: HEHD=HDHC
EHDˆ=CHBˆ(đối đỉnh)
Suy ra △HED∼△HBC(c – g – c)
Suy ra: D1ˆ=C1ˆ(1)
mà còn có: đường cao BD và CE cắt nhau tại H (gt)
III. BÀI TẬP CHỨNG MINH HAI TAM GIÁC ĐỒNG DẠNG
1. Bài tập có lời giải:
Bài 1: Cho ∆ABC có các đường cao BD và CE cắt nhau tại H. Chứng minh :
a) ∆HBE đồng dạng ∆HCE.
b) ∆HED đồng dạng ∆HBC và 
c) cho biết BD = CD. Gọi M là giao điểm của AH và BC. chứng minh : DE vuông góc EM.
Giải
a) xét ∆HBE và ∆HCD, ta có :
 (gt)
(gt)
 (đối đỉnh)
(đối đỉnh)
=> ∆HBE ~ ∆HCD (g – g)
b) ∆HED và ∆HBC, ta có :
 (∆HBE ~ ∆HCD)
(∆HBE ~ ∆HCD)
=> 
 (đối đỉnh)
(đối đỉnh)
=> ∆HED ~ ∆HBC (c – g – c)
=>  (1)
(1)
mà : Đường cao BD và CE cắt nhau tại H (gt)
=> H là trực tâm.
=> AH ⊥ BC tại M.
=> 
mặt khác: 
=>  (2)
(2)
từ (1) và (2) : 
hay: 
c) cmtt câu b, ta được: (3)
xét ∆BCD, ta có :
DB = DC (gt)
=> ∆BCD cân tại D
=>
mà: (∆HED ~ ∆HBC)
=>
mà:
(cmt)
=>
hay:
=> ED ⊥ EM.
Bài 2: Cho ∆ABC (AB < AC), có AD là đường phân giác trong. Ở miền ngoài ∆ABC vẽ tia Cx sao cho . Gọi I là giao điểm của Cx và AD. cmr :
a) ∆ADB đồng dạng ∆CDI.
b)
c) AD2 = AB.AC – BD.DC
Giải
a) ∆ADB và ∆CDI , ta có : (gt)
(đối đỉnh)
=> ∆ADB ~ ∆CDI
b) ∆ABD và ∆AIC , ta có : (∆ADB ~ ∆CDI)
(AD là phân giác)
=> ∆ABD ~ ∆AIC
=>
c) => AD.AI = AB.AC (1)
mà : (∆ADB ~ ∆CDI )
=> AD.DI = BD.CD (2)
từ (1) và (2) :AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI ) = AD.AD = AD2
Bài 3: Cho tam giác ABC vuông tại A, có đường cao AH . Chứng minh các hệ thức :
a. AB2 = BH.BC và AC2 = CH.BC
b. AB2 +AC2 = BC2
c. AH2 = BH.CH
d. AH.BC = AB.AC
Giải.
Xét hai ∆ABC và ∆ HAC, ta có:
a. AC2 = CH.BC :
là góc chung.
=> ∆ABC ~ ∆HAC (g – g)
=>
=> AC2 = CH.BC (1)
Cmtt : AB2 = BH.BC (2)
b. AB2 +AC2 = BC2
Từ (1) và (2), ta có :
AB2 +AC2 = BH.BC + CH.BC = (BH + CH)BC = BC2
c. AH2 = BH.CH :
Xét hai ∆HBA và ∆ HAC, ta có :
cùng phụ
=> ∆HBA ~ ∆HAC (g – g)
=>
=> AH2 = BH.CH
d. AH.BC = AB.AC :
Ta có : (∆ABC ~ ∆HAC)=> AH.BC = AB.AC.
Bài 4: Cho ∆ABC nhọn. kẻ đường cao BD và CE. vẽ các đường cao DF và EG của ∆ADE. Chứng minh
a) ∆ABD đồng dạng ∆AEG.
b) AD.AE = AB.AG = AC.AF
c) FG // BC
Giải
a) xét ∆ABD và ∆AEG, ta có :BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
=> BD // EG
=> ∆ABD ~ ∆AGE
b) =>
=> AD.AE = AB.AG (1)
cmtt, ta được : AD.AE = AC.AF (2)
từ (1) và (2) suy ra :AD.AE = AB.AG = AC.AF
c) xét ∆ABC, ta có :AB.AG = AC.AF (cmt)
=> FG // BC (định lí đảo talet)
Do đó H là trực tâm, suy ra AH⊥BC tại M.
Suy raA1ˆ+ABCˆ=90∘
Mặt khác : C1ˆ+ABCˆ=90∘
Suy ra: A1ˆ=C1ˆ (2)
Từ (1) và (2) => A1ˆ=D1ˆ
hay: HDEˆ=HAEˆ
2. Bài tập tự luyện thêm
Bài 1: Cho tam giác ABC vuông tại A , đường cao AH. Chứng minh:
a/ AH.BC = AB.AC
b/ AB² = BH.BC
c/ AH² = BH.CH
d/ Gọi M là trung điểm của BH, N là trung điểm của AH. Chứng minh: CN AM.
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền thành 2 đoạn BH = 9cm và HC = 16cm. Tính AB, AC, BC.
Bài 3: Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 21cm; AC = 28cm.
a/ Tính AH
b/ Kẻ HD AB; HE AC. Tính diện tích tam giác AED.
Bài 4: Cho tam giác ABC vuông tại A có AB = 15cm, AC = 20cm. Kẻ đường cao AH, trung tuyến AM.
a/ Tính AH; BC. b/ Tính BH,CH. c/ Tính diện tích tam giác AHM.
Bài 5: Cho có ba góc nhọn, đường cao AH. Vẽ HD vuông góc AB tại D, HE vuông góc AC tại E.
a) Chứng minh: tam giác AHB đồng dạng với tam giác ADH và tam giác AHC đồng dạng với tam giác AEH.
b) Chứng minh: AD.AB = AE.AC.
c) Cho AB = 12 cm, AC = 15 cm, BC = 18 cm. Tính độ dài đường phân giác AK của (K thuộc BC)
Bài 6: Cho ABC có AB = 3 cm, AC = 4 cm, BC = 5 cm. Đường phân giác góc A cắt cạnh BC tại D. Qua D vẽ đường thẳng vuông góc với BC cắt AC tại E và BA tại K.
a/ Chứng minh ABC vuông
b/ Tính DB, DC
c/ Chứng minh tam giác EDC đồng dạng với tam giác BDK
d/ Chứng minh DE = DB
Bài 7: Cho ABC vuông tại A, cho biết AB = 15 cm, AC = 20 cm. Kẻ đường cao AH của ABC.
a) Chứng minh: tam giác AHB đồng dạng với tam giác CAB và suy ra AB² = BH.BC
b) Tính độ dài các đoạn thẳng BH và CH.
c) Kẻ HM vuông góc với AB và HN vuông góc với AC. Chứng minh: AM.AB = AN.AC
d)Chứng minh: tam giác AMN đồng dạng với tam giác ACB
Bài 8: Cho tam giác ABC vuông tại A. Đường phân giác của góc A cắt cạnh huyền BC tại D. Qua D kẻ đường thẳng vuông góc với BC và cắt AC tại E.
a) Chứng minh tam giác DEC đồng dạng với tam giác ABC.
b) Chứng minh: DB = DE.
Bài 9: Cho tam giác ABC vuông tại A có AB = 16cm, BC = 20cm. Kẻ đường phân giác BD (D thuộc AC)
a) Tính CD và AD
b) Từ C kẻ CH vuông góc với BD tại H. Chứng minh: Tam giác ABD đồng dạng với tam giác HCD
c) Tính diện tích tam giác HCD .
Trên đây, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá.vn đã giới thiệu đến quý thầy cô và các bạn tam giác đồng dạng là gì ? Cách chứng minh hai tam giác đồng dạng nhanh nhất. Hi vọng, bài viết đã cung cấp cho bạn những thông tin hữu ích. Xem thêm cách chứng minh hình thang tại đường link này nhé !
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận! Nguồn chia sẻ: https://tmdl.edu.vn/tam-giac-dong-dang-la-gi-cach-chung-minh-hai-tam-giac-dong-dang/
Tam giác đồng dạng là gì ? Cách chứng minh hai tam giác đồng dạng
Chuyên đề về tam giác đồng dạng cũng như cách chứng minh hai tam giác đồng dạng học sinh đã được tìm hiểu trong chương trình Toán 8, phân môn Hình học. Đây là phần kiến thức vô cùng quan trọng của chương trình. Bài viết hôm nay, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá sẽ hệ thống lại tất cả các kiến thức cần ghi nhớ về chuyên đề này. Bạn tìm hiểu nhé !
I. LÝ THUYẾT VỀ TAM GIÁC ĐỒNG DẠNG
Bạn đang xem bài: Tam giác đồng dạng là gì ? Cách chứng minh hai tam giác đồng dạng
1. Định nghĩa hai tam giác đồng dạng
Hai tam giác đồng dạng là gì? “Đồng dạng” là từ Hán Việt và vốn có nghĩa là giống nhau. Hai tam giác đồng dạng với nhau khi chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Tam giác ABC và tam giác A’B’C’ được gọi là đồng dạng với nhau nếu: A^=A′^;B^=B′^;C^=C′^
và A′B′AB=B′C′BC=A′C′AC
Kí hiệu hai tam giác đồng dạng: △ABC∼△A′B′C′
Tỉ số: A′B′AB=B′C′BC=A′C′AC=k được gọi là tỉ số đồng dạng.

2. Các trường hợp đồng dạng của tam giác thường
- Trường hợp 1: Ba cạnh tương ứng tỉ lệ nhau (c – c – c).
Xét hai tam giác ABC và DEF có:
ABDE=ACDF=BCEF
Suy ra: △ABC∼△DEF (c – c – c)
- Trường hợp 2: Hai cạnh tương ứng tỉ lệ nhau – góc xen giữa hai cạnh bằng nhau (c – g – c).
Xét hai tam giác ABC và DEF, ta có:
ABDE=ACDF
A^=D^
Suy ra: △ABC∼△DEF (c – g – c)
- Trường hợp 3: Hai góc tương ứng bằng nhau (g – g)
Xét hai tam giác ABC và DEF có:
A^=D^
B^=E^
Suy ra: △ABC∼△DEF (g – g)

3. Các định lý đồng dạng của tam giác vuông
- Định lý 1: Cạnh huyền – Cạnh góc vuông
Nếu cạnh huyền và cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác đó đồng dạng.
- Định lý 2: Hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác đó đồng dạng.
- Định lý 3: Góc của hai tam giác vuông
Nếu góc nhọn của tam giác vuông này bằng góc nhọn của tam giác vuông kia thì hai tam giác đó đồng dạng.
II. CÁCH CHỨNG MINH HAI TAM GIÁC ĐỒNG DẠNG
Dạng 1 : Chứng minh hai tam giác đồng dạng – Hệ thức :
Bài toán: Cho △ABC(AB<AC), AD là đường phân giác trong. Miền ngoài △ vẽ tia Cx sao cho BCxˆ=BADˆ. Gọi I là giao điểm của Cx và AD. Chứng minh rằng:
- a) △ADB∼△CDI
- b) ADAC=ABAI
- c) AD2 = AB.AC – BD.DC
Cách giải:

a) Xét △ADB và △CDI , ta có:
BCxˆ=BADˆ (gt)
D1ˆ=D2ˆ (đối đỉnh)
Suy ra: △ADB∼△CDI
b) Xét △ABD và △AIC , ta có :
Bˆ=Iˆ (△ADB∼△CDI)
A1ˆ=A2ˆ(AD là phân giác)
Suy ra △ABD∼△AIC
Suy ra ADAC=ABAI, suy ra AD.AI = AB.AC (1)
c) Có ADCD=BDBI △ADB∼△CDI
Suy ra: AD.DI = BD.CD (2)
từ (1) và (2) :
Suy ra: AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI ) = AD.AD = AD2
Dạng 2: Chứng minh hai tam giác đồng dạng – Định lí Talet và Hai đường thẳng song song
Bài toán:
Cho tam giác ABC nhọn, đường cao BD và CE. Kẻ các đường cao DF và EG của tam giác ADE. Chứng minh:
- a) △ADB∼△AEG
- b) AD.AE = AB.AG = AC.AF
- c) FG // BC
Cách giải:

a) Xét tam giác ABD và AEG, ta có :
BD AC (BD là đường cao)
EG AC (EG là đường cao)
Suy ra: BD // EG
Suy ra: △ADB∼△AEG
b) Từ a) Suy raABAE=ADAG
⇒ AD.AE = AB.AG (1)
CM tương tự, ta được : AD.AE = AC.AF (2)
Từ (1) và (2) suy ra :
AD.AE = AB.AG = AC.AF
c) Xét tam giác ABC, ta có :
AB.AG = AC.AF (cmb) suy ra: ABAF=ACAG
Suy ra: FG // BC (định lí Talet đảo)
Dạng 3: Chứng minh hai tam giác đồng dạng – góc tương ứng bằng nhau
Bài toán: Cho tam giác ABC có các đường cao BD và CE cắt nhau tại H. Chứng minh:
- a) Tam giác HBE và tam giác HCE đồng dạng.
- b) △HED∼△HBC
và HDEˆ=HAEˆ
Cách giải:

a) Xét tam giác HBE và tam giác HCD, ta có :
BEHˆ=CDHˆ=90∘ (gt)
H1ˆ=H2ˆ (đối đỉnh)
Suy ra: △HBE∼△HCD (g – g)
b) Xét tam giác HED và HBC, ta có :
HEHD=HDHC (△HBE∼△HCD)
Suy ra: HEHD=HDHC
EHDˆ=CHBˆ(đối đỉnh)
Suy ra △HED∼△HBC(c – g – c)
Suy ra: D1ˆ=C1ˆ(1)
mà còn có: đường cao BD và CE cắt nhau tại H (gt)
III. BÀI TẬP CHỨNG MINH HAI TAM GIÁC ĐỒNG DẠNG
1. Bài tập có lời giải:
Bài 1: Cho ∆ABC có các đường cao BD và CE cắt nhau tại H. Chứng minh :
a) ∆HBE đồng dạng ∆HCE.
b) ∆HED đồng dạng ∆HBC và 
c) cho biết BD = CD. Gọi M là giao điểm của AH và BC. chứng minh : DE vuông góc EM.
Giải
a) xét ∆HBE và ∆HCD, ta có :
 (gt)
(gt)
 (đối đỉnh)
(đối đỉnh)
=> ∆HBE ~ ∆HCD (g – g)
b) ∆HED và ∆HBC, ta có :
 (∆HBE ~ ∆HCD)
(∆HBE ~ ∆HCD)
=> 
 (đối đỉnh)
(đối đỉnh)
=> ∆HED ~ ∆HBC (c – g – c)
=>  (1)
(1)
mà : Đường cao BD và CE cắt nhau tại H (gt)
=> H là trực tâm.
=> AH ⊥ BC tại M.
=> 
mặt khác: 
=>  (2)
(2)
từ (1) và (2) : 
hay: 
c) cmtt câu b, ta được: (3)
xét ∆BCD, ta có :
DB = DC (gt)
=> ∆BCD cân tại D
=>
mà: (∆HED ~ ∆HBC)
=>
mà:
(cmt)
=>
hay:
=> ED ⊥ EM.
Bài 2: Cho ∆ABC (AB < AC), có AD là đường phân giác trong. Ở miền ngoài ∆ABC vẽ tia Cx sao cho . Gọi I là giao điểm của Cx và AD. cmr :
a) ∆ADB đồng dạng ∆CDI.
b)
c) AD2 = AB.AC – BD.DC
Giải
a) ∆ADB và ∆CDI , ta có : (gt)
(đối đỉnh)
=> ∆ADB ~ ∆CDI
b) ∆ABD và ∆AIC , ta có : (∆ADB ~ ∆CDI)
(AD là phân giác)
=> ∆ABD ~ ∆AIC
=>
c) => AD.AI = AB.AC (1)
mà : (∆ADB ~ ∆CDI )
=> AD.DI = BD.CD (2)
từ (1) và (2) :AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI ) = AD.AD = AD2
Bài 3: Cho tam giác ABC vuông tại A, có đường cao AH . Chứng minh các hệ thức :
a. AB2 = BH.BC và AC2 = CH.BC
b. AB2 +AC2 = BC2
c. AH2 = BH.CH
d. AH.BC = AB.AC
Giải.
Xét hai ∆ABC và ∆ HAC, ta có:
a. AC2 = CH.BC :
là góc chung.
=> ∆ABC ~ ∆HAC (g – g)
=>
=> AC2 = CH.BC (1)
Cmtt : AB2 = BH.BC (2)
b. AB2 +AC2 = BC2
Từ (1) và (2), ta có :
AB2 +AC2 = BH.BC + CH.BC = (BH + CH)BC = BC2
c. AH2 = BH.CH :
Xét hai ∆HBA và ∆ HAC, ta có :
cùng phụ
=> ∆HBA ~ ∆HAC (g – g)
=>
=> AH2 = BH.CH
d. AH.BC = AB.AC :
Ta có : (∆ABC ~ ∆HAC)=> AH.BC = AB.AC.
Bài 4: Cho ∆ABC nhọn. kẻ đường cao BD và CE. vẽ các đường cao DF và EG của ∆ADE. Chứng minh
a) ∆ABD đồng dạng ∆AEG.
b) AD.AE = AB.AG = AC.AF
c) FG // BC
Giải
a) xét ∆ABD và ∆AEG, ta có :BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
=> BD // EG
=> ∆ABD ~ ∆AGE
b) =>
=> AD.AE = AB.AG (1)
cmtt, ta được : AD.AE = AC.AF (2)
từ (1) và (2) suy ra :AD.AE = AB.AG = AC.AF
c) xét ∆ABC, ta có :AB.AG = AC.AF (cmt)
=> FG // BC (định lí đảo talet)
Do đó H là trực tâm, suy ra AH⊥BC tại M.
Suy raA1ˆ+ABCˆ=90∘
Mặt khác : C1ˆ+ABCˆ=90∘
Suy ra: A1ˆ=C1ˆ (2)
Từ (1) và (2) => A1ˆ=D1ˆ
hay: HDEˆ=HAEˆ
2. Bài tập tự luyện thêm
Bài 1: Cho tam giác ABC vuông tại A , đường cao AH. Chứng minh:
a/ AH.BC = AB.AC
b/ AB² = BH.BC
c/ AH² = BH.CH
d/ Gọi M là trung điểm của BH, N là trung điểm của AH. Chứng minh: CN AM.
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền thành 2 đoạn BH = 9cm và HC = 16cm. Tính AB, AC, BC.
Bài 3: Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 21cm; AC = 28cm.
a/ Tính AH
b/ Kẻ HD AB; HE AC. Tính diện tích tam giác AED.
Bài 4: Cho tam giác ABC vuông tại A có AB = 15cm, AC = 20cm. Kẻ đường cao AH, trung tuyến AM.
a/ Tính AH; BC. b/ Tính BH,CH. c/ Tính diện tích tam giác AHM.
Bài 5: Cho có ba góc nhọn, đường cao AH. Vẽ HD vuông góc AB tại D, HE vuông góc AC tại E.
a) Chứng minh: tam giác AHB đồng dạng với tam giác ADH và tam giác AHC đồng dạng với tam giác AEH.
b) Chứng minh: AD.AB = AE.AC.
c) Cho AB = 12 cm, AC = 15 cm, BC = 18 cm. Tính độ dài đường phân giác AK của (K thuộc BC)
Bài 6: Cho ABC có AB = 3 cm, AC = 4 cm, BC = 5 cm. Đường phân giác góc A cắt cạnh BC tại D. Qua D vẽ đường thẳng vuông góc với BC cắt AC tại E và BA tại K.
a/ Chứng minh ABC vuông
b/ Tính DB, DC
c/ Chứng minh tam giác EDC đồng dạng với tam giác BDK
d/ Chứng minh DE = DB
Bài 7: Cho ABC vuông tại A, cho biết AB = 15 cm, AC = 20 cm. Kẻ đường cao AH của ABC.
a) Chứng minh: tam giác AHB đồng dạng với tam giác CAB và suy ra AB² = BH.BC
b) Tính độ dài các đoạn thẳng BH và CH.
c) Kẻ HM vuông góc với AB và HN vuông góc với AC. Chứng minh: AM.AB = AN.AC
d)Chứng minh: tam giác AMN đồng dạng với tam giác ACB
Bài 8: Cho tam giác ABC vuông tại A. Đường phân giác của góc A cắt cạnh huyền BC tại D. Qua D kẻ đường thẳng vuông góc với BC và cắt AC tại E.
a) Chứng minh tam giác DEC đồng dạng với tam giác ABC.
b) Chứng minh: DB = DE.
Bài 9: Cho tam giác ABC vuông tại A có AB = 16cm, BC = 20cm. Kẻ đường phân giác BD (D thuộc AC)
a) Tính CD và AD
b) Từ C kẻ CH vuông góc với BD tại H. Chứng minh: Tam giác ABD đồng dạng với tam giác HCD
c) Tính diện tích tam giác HCD .
Trên đây, Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá.vn đã giới thiệu đến quý thầy cô và các bạn tam giác đồng dạng là gì ? Cách chứng minh hai tam giác đồng dạng nhanh nhất. Hi vọng, bài viết đã cung cấp cho bạn những thông tin hữu ích. Xem thêm cách chứng minh hình thang tại đường link này nhé !
Bản quyền bài viết thuộc Trường Trung Cấp Nghề Thương Mại Du Lịch Thanh Hoá. Mọi hành vi sao chép đều là gian lận! Nguồn chia sẻ: https://tmdl.edu.vn/tam-giac-dong-dang-la-gi-cach-chung-minh-hai-tam-giac-dong-dang/
Trang chủ: tmdl.edu.vn Danh mục bài: Giáo dục
