Bài viết này hướng dẫn cách chứng minh hình bình hành thông qua những tính chất của nó.
Hình học là một đề tài rộng lớn, chúng ta bắt gặp hình học xung quanh ta, vậy làm sao để biết được sâu hơn và hiểu rõ hơn về chúng thì hôm nay mình và các bạn sẽ cùng nhau tìm hiểu và cụ thể hơn đó chính là chúng ta sẽ tìm ra cách chứng minh hình bình hành trong bài viết này nhé.
1. Các tính chất của hình bình hành
Hình bình hành là một hình tứ giác có hai cặp cạnh đối song song.
Muốn chứng minh hình bình hành thì việc chúng ta nắm chắc tính chất của hình bình hành là rất quan trọng, nó là tiền đề giúp các bạn chứng minh được hình bình hành một cách đơn giản và chính xác nhất.
Bài viết này được đăng tại [free tuts .net]
Một hình bình hành sẽ có những tính chất sau:
- Hình bình hành là hình có các cạnh đối song song và bằng nhau
- Trong một hình tứ giác có các góc đối bằng nhau thì đấy cũng là một trong những tính chất của hình bình hành
- Hình bình hành là hình có hai đường chéo cắt nhau tại trung điểm của mỗi đường
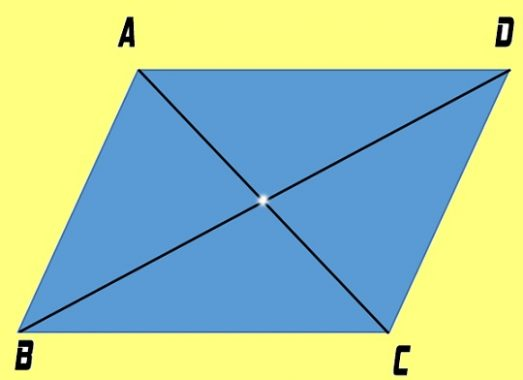
Nhìn hình vẽ đã cho và dựa vào khái niệm chúng ta có hình tứ giác ABCD chính là một hình bình hành có cạnh AB // DC và cạnh AD // BC.
Từ đây chúng ta thấy được rằng hình bình hành là một dạng đặc biệt của hình thang, nó chính là hình thang có hai cạnh bên song song.
Vậy làm sao để chúng ta có thể chứng minh được một hình tứ giác chính là hình bình hành? Phần tiếp theo sẽ giúp các bạn giải đáp nhé.
2. Cách chứng minh hình bình hành đơn giản nhất
Có nhiều cách để chứng minh một hình tứ giác là hình bình hành. Chúng ta có thể áp dụng tính chất nó là một tứ giác có các cặp cạnh đối diện song song, là tức giác có các cặp cạnh đối bằng nhau …
Cách 1: Tứ giác có các cạnh đối song song là hình bình hành
Muốn chứng minh được một hình tứ giác là hình bình hành thì chúng ta cần chứng minh được tứ giác đó có hai cặp cạnh đối song song.
Ví dụ: Cho tứ giác ABCD như hình dưới đây:
- Điểm E là trung điểm của đoạn thẳng AB.
- Điểm F là trung điểm của đoạn thẳng BC.
- Điểm G là trung điểm của đoạn thẳng DC.
- Điểm H là trung điểm của đoạn thẳng AD.
Các bạn hãy cho biết tứ giác EFGH là hình gì? Chứng minh điều đó?
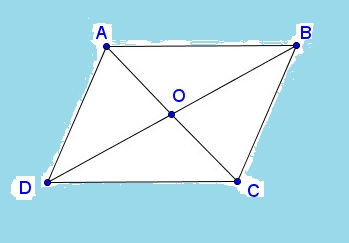
Sau khi vẽ hình và nhìn vào hình vẽ, chúng ta có:
- EF là đường trung bình của tam giác ABC, nên ta suy ra được EF // AC (dữ liệu 1)
- HG là đường trung bình của tam giác ADC, nên ta suy ra được HG // AC (dữ liệu 2)
- Từ hai dữ liệu 1 và 2 chúng ta có thể biết được rằng EF//HC
Tiếp theo chúng ta có:
- FG là đường trung bình của tam giác BDC, nên FG // BD (Dữ liệu 3)
- EH là đường trung bình của tam giác BDA, nên EH // BD (dữ liệu 4)
- Từ dữ liệu 3 và 4 chúng ta có thể biết được cạnh FG // EH.
Chúng ta xét tứ giác EFGH và thấy được rằng cạnh EF // HG và FG // EH.
Hình tứ giác EFGH là hình bình hành vì nó có hai cặp cạnh đối song song (điều phải chứng minh)
Cách 2: Tứ giác có các cạnh đối bằng nhau là hình bình hành
Để chứng minh được tứ giác đó là một hình bình hành thì chúng ta có thể chứng minh nó có các cạnh đối bằng nhau.
Ví dụ: Cho một tứ giác ABCD như hình dưới đây, trong đó có tam giác ABC = tam giác ADC. Bạn hãy chứng minh tứ giác ABCD chính là hình bình hành?
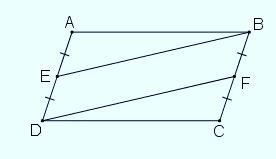
Vì đề bài đã cho và dựa theo hình vẽ, tam giác ABC = tam giác ADC nên:
AD=BC và AB=DC
Từ đây suy ra được rằng tứ giác ABCD chính là hình bình hành (vì có các cặp cạnh đối bằng nhau).
Cách 3: Tứ giác có hai cạnh đối song song và bằng nhau thì được gọi là hình bình hành
Chúng ta có ví dụ sau: Hình bình hành ABCD có F là trung điểm của BC và E là trung điểm của AD. Hãy chứng minh tứ giác EBFD là hình bình hành?
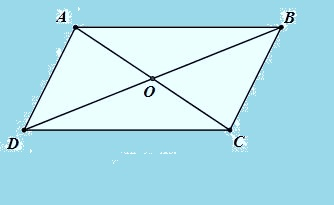
Vì ABCD là hình bình hành nên chúng ta có AD//BC và AD=BC
Vì AD // BC nên ED // BF (dữ liệu 1)
Chúng ta lại có E là trung điểm của AD nên sẽ chia đoạn thẳng AD thành hai phần bằng nhau ED = EA và F là trung điểm của BC nên chia đoạn thẳng BC thành hai phần bằng nhau FB = FC.
ABCD là hình bình hành nên chúng ta có ED=EA=FB=FC, suy ra ED = FB (dữ liệu 2)
Từ dữ liệu 1 và 2 chúng ta có thể kết luận rằng tứ giác EBFD là hình bình hành( vì có các cặp cạnh đối song song và bằng nhau)
Cách 4: Tứ giác có các góc đối bằng nhau là hình bình hành
Để chứng minh hình bình hành chúng ta có thể tìm các góc đối bằng nhau
Ví dụ: Cho hình tứ giác ABCD có tam giác ABC = tam giác ADC, tam giác ADB = tam giác CDB. Hãy chứng minh tứ giác trên chính là hình bình hành?
Dựa theo đề bài đã cho chúng ta có:
- Tam giác ABC= tam giác ADC nên góc B= góc D(1)
- Tam giác ADB = tam giác CDB nên góc A= góc C(2)
- Từ 1 và 2 chúng ta có thể kết luận rằng tứ giác ABCD chính là hình bình hành vì nó có các góc đối bằng nhau.
Cách 5: Hình bình hành là hình có hai đường chéo cắt nhau tại trung điểm mỗi đường
Ngoài những cách mà mình đã giới thiệu trên thì chúng ta còn một cách nữa đó chính là chứng minh được tứ giác đó có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó chính là hình bình hành
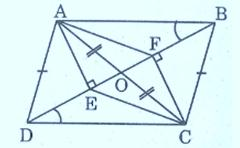
Ví dụ: Cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O. Kẻ thêm đường AE vuông góc với BD và CF vuông góc với BD. Hãy chứng minh rằng tứ giác AFCE là hình bình hành.
Áp dụng tính chất của hình bình hành chúng ta có AO=OC(1).
Xét tam giác vuông AOE và AOF có:
- Góc E= góc F= 90 độ vì góc AOE= góc AOF( hai đỉnh đối nhau)
Từ đó suy ra được tam giác AOE= tam giác COF nên cạnh OE=OF(2)
Từ(1) và (2) ta kết luận được rằng tứ giác AECE là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
3. Một số câu hỏi liên quan đến hình bình hành
Khái niệm hình bình hành
Hình bình hành là một hình tứ giác có các cặp cạnh đối vừa song song và bằng nhau thì được gọi là hình bình hành.
Tính chất của hình bình hành
Nếu một tứ giác là hình bình hành thì sẽ có những tính chất sau:
- Các cặp cạnh đối của hình bình hành sẽ bằng nhau
- Các góc đối của hình bình hành sẽ là các góc bằng nhau
- Hai đường chéo của hình bình hành sẽ cắt nhau tại trung điểm của mỗi đường
Các dấu hiệu nhận biết hình bình hành
Hãy kết luận ngay hình tứ giác đó là hình bình hành khi bạn gặp các dấu hiệu sau:
- Hình tứ giác có các cạnh đối song song với nhau
- Các cạnh đối của hình tứ giác đó bằng nhau
- Các góc đối của hình tứ giác đó bằng nhau
- Hai đường chéo của hình tứ giác đó cắt nhau tại trung điểm của mỗi đường
- Tứ giác có hai cạnh đối vừa song song vừa bằng nhau
Quy tắc hình bình hành
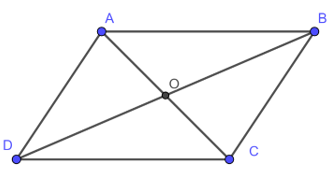
Cho hình bình hành ABCD và giao điểm của hai đường chéo cắt nhau tại O.
AB + AD=AC
Chúng ta có quy tắc sau: Tổng của hai vecto cạnh có điểm xuất phát trùng nhau của hình bình hành sẽ bằng vecto đường chéo có điểm xuất phát trùng với điểm xuất phát của hai cạnh trên.
Chúng ta có thể chứng minh hình bình hành dựa vào hai vecto bằng nhau và quy tắc 3 điểm
- Vì ABCD là hình bình hành nên AD = BC
- Chính vì thế ta có: AD + AB = AB + BC = AC
Trên đây chính là quy tắc hình bình hành mình muốn gửi đến các bạn, mong rằng các bạn sẽ vận dụng thật tốt quy tắc trên để giải được các bài toán có liên quan.
Trên đây là 5 cách chứng minh một hình tứ giác là hình bình hành, các bạn hãy áp dụng nó thật tốt để thực hiện các bài giải toán về chứng minh hình bình hành nhé. Chúc các bạn đạt điểm tối đa.
