Đa thức là gì? Bậc của đa thức là gì? Các dạng toán về đa thức là những lý thuyết được rất nhiều bạn học sinh quan tâm. Mời các bạn theo dõi bài viết sau đây để cùng thapgiainhietliangchi đi tìm hiểu về đa thức nhé!
Tìm hiểu về đa thức là gì?
Đa thức là gì?
Đa thức chính là một tổng của hai hay nhiều đơn thức gộp lại với nhau. Mỗi đơn thức trong tổng sẽ được gọi là một hạng tử của đa thức đó. Mỗi đơn thức cũng có thể được coi là đa thức.
Ví dụ minh họa đa thức là gì: 5xy + 7y + 4 là một đa thức.

Phân biệt đa thức với đơn thức
- Đa thức là một biểu thức toán học được hình thành từ tổng của các đơn thức lại với nhau.
- Đơn thức sẽ không thể có một phép cộng hoặc phép trừ giữa các biến được.
- Bậc của đa thức sẽ là là bậc của đơn thức cao nhất.
Đa thức 1 biến là gì?
Đa thức 1 biến là gì? Đa thức 1 biến là tổng của những đơn thức của có cùng một biến.
Lưu ý: Ta có một số được coi là đa thức một biến.
Một đa thức 1 biến có các khả năng có 1 nghiệm, nhiều nghiệm hoặc không có nghiệm.
Số nghiệm tối đa của đa thức 1 biến sẽ không vượt quá bậc của đa thức đó.
Ví dụ minh họa đa thức 1 biến là gì: y² + 5y + 10 là một đa thức một biến.

Nghiệm của đa thức là gì?

Các bài toán về đa thức chủ yếu là tìm các nghiệm của đa thức là gì, cũng là nghiệm của phương trình đại số, vì nếu ta có x là nghiệm của đa thức f(x) và làm cho đa thức này bằng 0. Bên cạnh đó x cũng là nghiệm của đa thức g(x) và làm cho g(x) bằng 0 suy ra f(x)=g(x)=0 và vì thế x sẽ là nghiệm của phương trình f(x)=g(x).
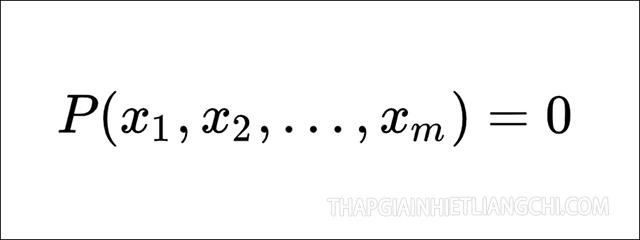
Nên đa thức của m biến sẽ được nhiều người gọi là đa thức của m ẩn.
Thu gọn đa thức là gì? Cách thu gọn đa thức thực hiện ra sao?
Thu gọn đa thức là việc thực hiện đưa đa thức về dạng thu gọn nhất (không còn hai hạng tử nào đồng dạng nữa)
Cách thu gọn đa thức là ta thu gọn các đơn thức với nhau qua 2 bước đơn giản sau:
Bước 1: Ta nhóm các đơn thức đồng dạng lại với nhau.
Bước 2: Tiến hành cộng, trừ các đơn thức đồng dạng trong từng nhóm đã tạo ở trên.
Các phép tính toán khác đa thức
Phép cộng đa thức như thế nào?
Muốn cộng hai đa thức lại với nhau ta thực hiện tuần tự các bước sau đây:
Bước 1: Viết liên tiếp hay gộp các hạng tử của hai đa thức đó cùng với dấu của chúng.
Bước 2: Tiến hành thu gọn các hạng tử đồng dạng lại (nếu có).
Ví dụ minh họa cộng đa thức
Tính toán đa thức sau : (x + 4y) +(3x – y)
Đầu tiên ta gộp các hạng tử cùng biến lại với nhau như sau:
(x + 4y) +(3x – y) = (x + 3x) + (4y – y) = 5x + 3y
Phép trừ đa thức như thế nào?
Muốn trừ thực hiện hai đa thức ta thực hiện tuần tự các bước sau:
Bước 1: Gộp các hạng tử của đa thức thứ nhất cùng với dấu của chúng.
Bước 2: Gộp tiếp các hạng tử của đa thức thứ hai với dấu ngược lại dấu ban đầu.
Bước 3: Tiến hành thu gọn các hạng tử đồng dạng lại với nhau (nếu có).
Ví dụ minh họa về phép trừ đa thức:
Tính toán đa thức (x + 2y) – (2x – y)
Đa thức đầu tiên không có dấu nên ta giữ nguyên, đa thức thứ hai có dấu trừ phía trước nên ta đổi dấu các đơn thức trong ngoặc như sau:
(x + 2y) – (2x – y) = x + 2y – 2x + y = (x – 2x) + (2y + y) = -x + 3y
Phép nhân đa thức như thế nào?
– Nhân đơn thức với đa thức: Để thực hiện ta nhân đơn thức với từng hạng tử của đa thức sau đó cộng tổng chúng lại với nhau.
Công thức tổng quát như sau: A(B + C) = AB + AC
Ví dụ minh họa phép nhân đa thức: x(6y + 5) = 6xy + 5x
– Nhân đa thức với đa thức: Để thực hiện ta lần lượt lấy từng hạng tử của đa thức này nhân với các hạng tử của đa thức kia, sau đó cộng tổng chúng lại với nhau.
Công thức: (A + B)(C + D) = AC + AD + BC + BD
Ví dụ minh họa phép nhân đa thức: (x + 2)(3y + 4) = 14x + 3xy + 6y + 8
Phép chia đa thức như thế nào?
- Chia đa thức cho đơn thức: Để thực hiện lần lượt lấy từng hạng tử của đa thức chia cho đơn thức sau đó cộng tổng chúng lại với nhau.
Ví dụ minh họa phép chia đa thức:
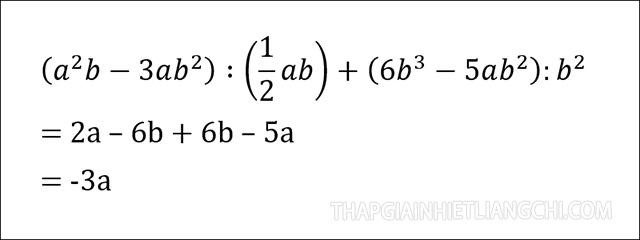
- Chia đa thức cho đa thức: Ta thực hiện sắp xếp đa thức theo lũy thừa giảm dần của biến, sau đó sẽ thực hiện phép chia.
Ví dụ minh họa phép chia đa thức:

Bậc của đa thức là gì?
Bậc của đa thức là gì? Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn rồi của đa thức đó.
Ví dụ minh họa bậc của đa thức là gì?
2×4 – 3x² – 3x² – 2 + 6x = 2×4 – 6x² + 6x -2 bậc của đa thức này là 4
Phương pháp để phân tích đa thức thành dạng nhân tử
- Phân tích đa thức thành các nhân tử bằng phương pháp đặt nhân tử chung: Đây là một cách làm phổ biến nhất và được nghĩ đến đầu tiên trong tất cả các phương pháp để phân tích nhân tử. Vì thế, cần chú ý và luyện tập phản xạ để phát hiện ra nhân tử chung một cách chính xác và nhanh nhất.
- Phân tích đa thức thành các nhân tử bằng cách dùng hằng đẳng thức: Bằng hãy cách nhận dạng các hằng đẳng thức, sau đó áp dụng vào để phân tích đa thức đó.
- Phân tích đa thức thành các nhân tử bằng cách nhóm nhiều hạng tử: Đây là phương pháp kết hợp tư duy của cả hai phương pháp đề cập đến ở trên.
- Thêm bớt một hạng tử hay tách hạng tử để phân tích thành các nhân tử: Phương pháp này đòi hỏi sự tư duy toán học cao hơn và sử dụng thuần thục những phương pháp trên mới có khả năng áp dụng.
Lưu ý ta cần phối hợp nhiều phương pháp lại một cách linh động để phân tích đa thức thành nhân tử một cách nhanh chóng, chính xác.
Các dạng toán về đa thức thường gặp nhất
Nhận biết đa thức
Căn cứ vào định nghĩa của đa thức là tổng của các đơn thức lại với nhau.
Thu gọn đa thức
Cách thu gọn đơn thức qua 2 bước đơn giản như sau:
Bước 1: Nhóm các đơn thức có đồng dạng lại với nhau.
Bước 2: Cộng, trừ các đơn thức đồng dạng trong từng nhóm đã nhóm ở trên.
Xem thêm: Đơn thức là gì? Bậc của đơn thức là gì? Bài tập về đơn thức
Tìm bậc của đa thức
Với dạng toán này, ta chỉ cần thực hiện với 2 bước đơn giản như sau:
Bước 1: Viết đa thức đó về dưới dạng thu gọn (nếu cần).
Bước 2: Bậc của đa thức sẽ là bậc của hạng tử có bậc cao nhất trong dạng thu gọn nhất của đa thức đó.
Một số bài tập áp dụng về đa thức
Bài tập 1: Sắp xếp đa thức 2x + 5x³ – x² + 5×4 theo lũy thừa giảm dần của biến x
- 5×4 – x² + 5x³ + 2x
- 2x – x² + 5x³ + 5×4
- 5×4 + 5x³ + x² – 2x
- 5×4 + 5x³ – x² + 2x
Ta có 2x + 5x³ – x² + 5×4 = 5×4 + 5x³ – x² + 2x
Đáp án đúng là đáp án D
Bài tập 2: Xác định bậc của đa thức xy + xy5 + x5yz là
- 6
- 7
- 5
- 4
Bậc của đa thức xy + xy5 + x5yz là 5 + 1 + 1 = 7
Chọn đáp án B là đáp án đúng.
Bài tập 3: Bạn hãy thu gọn đa thức sau: 4x²y + 6x³y² – 10x²y + 4x³y²
- 14x²y + 10x³y²
- -14x²y + 10x³y²
- 6x²y – 10x³y²
- -6x²y + 10x³y²
Ta có: 4x²y + 6x³y² – 10x²y + 4x³y²
= (4x²y – 10x²y ) + (6x³y² + 4x³y²) = -6x²y + 10x³y²
Chọn đáp án D là đáp án đúng cho câu hỏi này.
Bài viết trên đây là những kiến thức tổng quát về hàm đa thức là gì? Hy vọng qua bài viết các bạn đã hiểu được đa thức, áp dụng tốt trong các dạng bài tập để có kết quả học tập tốt nhất. Nếu còn thắc mắc nào về đa thức hãy để lại bình luận cho chúng tôi nhé!
