Bài này sẽ tổng hợp kiến thức về hình hộp chữ nhật như: Cách tính diện tích, tính chu vi hình hộp chữ nhật, tính thể tích hình hộp chữ nhật, tính đường chéo hình hộp chữ nhật.
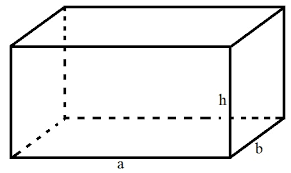
Đến với hình học không gian thì hình hộp chữ nhật là một dạng hình cơ bản và là khối hình học không gian đầu tiên mà các bạn làm quen, nó là tiền đề để giúp các em học sâu hơn và nâng cao hơn về hình học không gian sau này. Vậy ngày hôm nay, chúng ta cùng nhau tìm hiểu về khái niệm, tính chất và cách tính thể tích của hình hộp chữ nhật nhé.
1. Hình hộp chữ nhật là gì?
Hình hộp chữ nhật chính là một khối hình học không gian, nó được cấu tạo bởi 6 mặt phẳng hình chữ nhật, nó gồm có 8 đỉnh và 12 cạnh. Nói cách khác, nó được cấu tạo bởi nhiều hình chữ nhật hoặc hình vuông khác nhau.
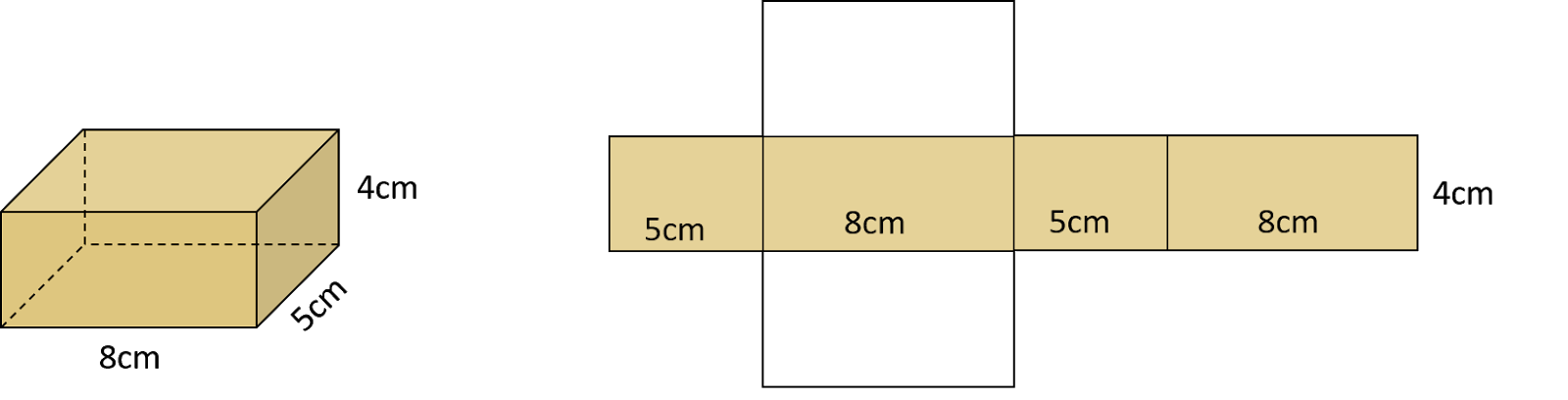
Bài viết này được đăng tại [free tuts .net]
Hai mặt phẳng song song với nhau được gọi là hai mặt đối diện của hình hộp chữ nhật. Như vậy chúng ta thấy rằng hình hộp chữ nhật gồm có 3 cặp mặt phẳng đối diện với nhau, trong đó có một cặp mặt phẳng đáy và hai cặp mặt phẳng bên.
Để tính diện tích của hình hộp chữ nhật thì ta sẽ áp dụng công thức tính diện tích hình chữ nhật cho 6 mặt phẳng, sau đó tùy vào yêu cầu của bài toán mà cộng chúng lại với nhau. Ngoài ra, chúng ta vẫn có thêm một số bài toán thường gặp nữa như: Tính chu vi, tính thể tính, tính độ dài đường chéo.
2. Các tính chất của hình hộp chữ nhật
Cũng tương tự như các hình khác thì hình hộp chữ nhật cũng có tính chất riêng của nó:
- Hình hộp chữ nhật là hình có 12 cạnh, 8 đỉnh và 6 mặt
- Các đường chéo của hình hộp chữ nhật có hai đầu mút là hai đỉnh đối nhau của hình hộp chữ nhật đồng quy tại một điểm
- Trong hình hộp chữ nhật thì diện tích của hai mặt đối diện nhau bằng nhau
- Hai mặt đối diện trong hình hộp chữ nhật có chu vi bằng nhau
3. Cách tính chu vi của hình hộp chữ nhật
Chu vi hình hộp chữ nhật chính là tổng độ dài của tất cả các cạnh tạo nên hình hộp chữ nhật đó. Dựa vào khái niệm này chúng ta có công thức tính chu vi của hình hộp chữ nhật như sau:
Chu vi của hình hộp chữ nhật bằng bốn lần tổng của chiều cao, chiều dài và chiều rộng của hình hộp chữ nhật đó.
Xét hình sau:
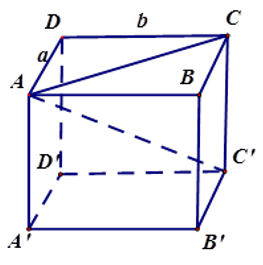
Ta có công thức tổng quát:
(!! C= 4(h+a+b) !!)
Trong đó :
- C là kí hiệu chu vi của hình hộp chữ nhật
- h là chiều cao của hình hộp chữ nhật đó
- a là chiều dài của hhcn
- b là chiều rộng của hhcn
Ví dụ: Cho một hình hộp chữ nhất chiều dài là 4cm, chiều rộng của nó là 2cm và chiều cao của hình hộp chữ nhật đó bằng một nửa tổng độ dài của chiều dài và chiều rộng. Hãy tính chu vi của hình hộp chữ nhật đó?
Bài giải: Trước tiên ta cần tính chiều cao đã nhé.
Chiều cao của hình hộp chữ nhật đó là:
(!! h = (4+2) div 2= 3 (cm) !!)
Vậy, chu vi của hình hộp chữ nhật đó là:
(!! C = 4 times (4+2+3)= 36 (cm) !!)
Đáp số : 36(cm)
4. Cách tính diện tích của hình hộp chữ nhật
Diên tích được chia làm hai loại, thứ nhất là diện tích xung quanh, và thứ hai là diện tích toàn phần.
Diện tích xung quanh
Nhắc đến từ xung quanh chúng ta hiểu rằng diện tích xung quanh chính là rổng diện tích các hình chữ nhật bao xung quanh của hình hộp chữ nhật đó. Hay chính xác hơn nó là tổng diện tích 4 mặt bên của hình hộp chữ nhật.
Chúng ta rút ra được kết luận sau:
Muốn tính diện tích xung quanh của hình hộp chữ nhật chúng ta lấy chu vi mặt đáy nhân với chiều cao( cùng đơn vị đo).
Công thức tổng quát
(!! Sxq = 2h(a+b) !!)
Trong đó:
- Sxq là diện tích xung quanh
- h là chiều cao của hình hộp chữ nhật
- a là chiều dài của hình hộp chữ nhật
- b là chiều rộng của hình hộp chữ nhật
Ví dụ: Cho hình hộp chữ nhật có chiều dài 8cm, chiều rộng 5cm và chiều cao là 6cm. Tính diện tích xung quanh của hình hộp chữ nhật đó?
Bài giải:
Diện tích xung quanh của hình hộp chữ nhật đó là:
(!! Sxq = 26(8+5)=156(cm^2) !!)
Đáp số: 156 cm2
Diện tích toàn phần của hình hộp chữ nhật
Diện tích toàn phần của hình hộp chữ nhật chính là tổng diện tích của tất cả các mặt phẳng hình chữ nhật tạo nên hình hộp chữ nhật đó.
Muốn tính diện tích toàn phần của hình hộp chữ nhật chúng ta lấy diện tích xung quanh cộng tổng diện tích của hai mặt đáy
Công thức tổng quát:
(!! Stp= Sxq + S2đáy !!)
Trong đó:
- Stp là diện toàn phần
- Sxq là diện tích xung quanh
- S2đáy là diện tích hai mặt đáy của hình hộp chữ nhật
Ví dụ: Cho một phòng học hình hộp chữ nhật có chiều dài là 7m, chiều rộng là 5m và chiều cao của phòng học là 4m. Tính diện tích toàn phần của căn phòng đó?
Bài giải:
Diện tích xung quanh của căn phòng đó là:
(!! Stp = 2 times 4 times (7+5)=96(m^2) !!)
Tổng diện tích hai đáy của căn phòng đó là:
(!! S2đáy = 2 times 7 times 5= 70(m^2) !!)
Diện tích toàn phần của căn phòng đó là:
(!! Stp = 96+70= 166(m^2) !!)
Đáp số: 166 m2
5. Cách tính thể tích của hình hộp chữ nhật
Thể tích hình hộp chữ nhật chính là lượng không gian mà hình đó chiếm phải.
Muốn tính thể tích của hình hộp chữ nhật chúng ta lấy diện tích đáy nhân với chiều cao của hình hộp chữ nhật đó. Hay nói cách khác thể tích hình hộp chữ nhật bằng tích của diện tích đáy và chiều cao.

Công thức tổng quát: (! V= a times b times h !)
Trong đó:
- V là thể tích
- a là chiều dài
- b là chiều rộng
- h là chiều cao
Đơn vị đo của thể tích là cen ti mét khối: (! cm^3 !)
Ví dụ: Cho hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao lần lượt là 12cm, 7cm và 8cm. Tính thể tích của hình hộp chữ nhật đó?
Bài giải:
Thể tích của hình hộp chữ nhật đó là:
(!! V = 12 times 7 times 8= 672(cm^3) !!)
Đáp số: 672 cm3
6. Công thức tính đường chéo của hình hộp chữ nhật
Đối với hình hộp chữ nhật chúng ta có thêm khái niệm về đường chéo. Các đường chéo của hình hộp chữ nhật là bằng nhau, vì vậy ta chỉ cần tính một kết quả là suy ra cho cả ba.
Công thức như sau:
(!! D = sqrt{a^2+b^2+h^2} !!)
Trong đó:
- D là độ dài đường chéo
- a là độ dài hình hộp chữ nhật
- b là chiều rộng hình hộp chữ nhật
- h là chiều cao của hình hộp chữ nhật
Ví dụ: Cho hình hộp chữ nhật ABCD. Có chiều dài, chiều rộng và chiều cao lần lượt là 15cm, 12cm và 8 cm. Tính độ dài đường chéo của hình hộp chữ nhật đó?
Bài giải:
Độ dài đường chéo của hình hộp chữ nhật đó là:
(!! D = sqrt{15^2+ 12^2+8^2}= 20,8 (cm) !!)
Đáp số: 20,8 cm
7. Một số bài toán về hình hộp chữ nhật
Bài toán 1: Người thợ làm một chiếc thùng có hình dạng là một hình hộp chữ nhật. chiếc thùng đó có độ dài là 3m, chiều rộng là 2, và chiều cao của chiếc thùng là 2,5m. Vậy người thợ đó cần bao nhiêu tôn để làm được chiếc thùng đó?
Bài giải: Đây là bài toán tính diện tích toàn phần.
Diện tích xung quanh của chiếc thùng đó là:
(!! Sxq = 2 times 2,5 times (3+2)= 25(m^2) !!)
Diện tích của hai mặt đáy chiếc thùng đó là:
(!! S2đáy = 2 times 3 times 2= 12(m^2) !!)
Gọi Stp là số tôn người thợ cần dùng, vậy Stp được tính như sau:
(!! Stp = 25+12=37(m^2) !!)
Đáp số: 37 m2
Bài toán 2: Một căn phòng hình chữ nhật có chiều dài là 7m, chiều rộng ít hơn chiều dài hai mét và có chiều cao bằng một nửa tổng số đo chiều dài và chiều rộng. Hỏi diện tích cần sơn căn phòng đó là bao nhiêu biết rằng tổng diện tích các cửa là 6m2.
Bài giải:
Chiều rộng của căn phòng đó là:
(!! b = 7-2 =5 (m) !!)
Chiều cao của căn phòng đó là:
(!! h = (7+5) div 2= 6(m) !!)
Diện tích xung quanh của căn phòng đó là:
(!! Sxq = 2 times 6 times (7+5)= 144(m^2) !!)
Diện tích nền nhà và trần nhà của căn phòng đó là (ta đặt ký hiệu là S2đáy):
(!! S2đáy = 2 times 7 times 5=70(m2) !!)
Diện tích mà căn phòng đó cần phải sơn là (ta đặt ký hiệu là Stp):
(!! Stp = (144+70) – 6= 208 (m^2) !!)
Đáp số: 208 m2
Bài toán 3: Một bể bơi hình hộp chữ nhật có chiều dài là 10m, chiều rộng là 6m và chiều cao là 3m. Hỏi người ta phải bơm vào bao nhiêu mét khối nước mới làm cho cái bể bơi đó đầy?
Bài giải:
Số mét khối nước mà họ cần bơm vào bể là:
(!! V = 10 times 6 times 3= 180(m^3) !!)
Đáp số: 180 m3
Lời kết:
Trên đây mình đã giới thiệu và tổng hợp các bài toán về hình hộp chữ nhật như:
- Cách tính chu vi hình hộp chữ nhật.
- Cách tính diện tích hình hộp chữ nhật (diện tích toàn phần và diện tích xung quanh)
- Cách tính thể tích hình hộp chữ nhật.
- Cách tính độ dài đường chéo hình hộp chữ nhật.
- Và các bài toán về hình hộp chữ nhật thường gặp.
Chúc bạn học tốt nhé.
