Cách tính góc giữa đường thẳng và mặt phẳng lớp 11

Bài toán xác định góc giữa đường thẳng và mặt phẳng là một dạng toán quan trọng của chương trình HHKG lớp 11. Bài toán này cùng với các bài toán tính góc giữa 2 mặt phẳng, khoảng cách từ điểm tới mặt phẳng đều sử dụng kiến thức về đường thẳng vuông góc với mặt phẳng.

Xem thêm:

• Cách chứng minh đường thẳng vuông góc với mặt phẳng
• Cách tính góc giữa hai mặt phẳng trong không gian
• Cách tính khoảng cách từ một điểm đến một mặt phẳng
• 38+ tài liệu hình học không gian 11 hay nhất

1. Lý thuyết góc giữa đường thẳng và mặt phẳng

Định nghĩa góc giữa đường thẳng và mặt phẳng trong không gian

• Nếu đường thẳng vuông góc với mặt phẳng thì ta góc giữa đường thẳng và mặt phẳng bằng 90°.
• Nếu đường thẳng không vuông góc với mặt phẳng thì góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng .

Kí hiệu góc giữa đường thẳng $d$ và mặt phẳng $(P)$ là ( left(d,(P)right) ).

Nhận xét.

• Góc giữa đường thẳng và mặt phẳng có số đo từ từ ( 0^circ ) đến ( 90^circ )
• Đường thẳng song song hoặc nằm trong mặt phẳng thì góc giữa chúng bằng ( 0^circ )

2. Cách xác định góc giữa đường thẳng và mặt phẳng

Bài toán. Xác định góc giữa đường thẳng $d$ và mặt phẳng $(P)$

Trong thực tế, chúng ta ít khi gặp tình huống đường thẳng $d$ song song với mặt phẳng $(P)$ hoặc nằm trong mặt phẳng $(P)$, vì khi đó góc giữa chúng bằng $0^circ$. Còn nếu đường thẳng $d$ vuông góc với mặt phẳng $(P)$ thì góc giữa chúng bằng $90^circ$. Trường hợp còn lại, đường thẳng $d$ sẽ cắt và không vuông góc với $(P)$. Khi đó, chúng ta thực hiện 3 bước:

• Tìm giao điểm của đường thẳng $d$ và mặt phẳng $ (P)$, giả sử là điểm $ O $;
• Lấy một điểm $ A$ bất kì thuộc đường thẳng $ d$ và tìm hình chiếu vuông góc $ H$ của $ A$ lên $left( Pright)$;
• Tính góc $ widehat{AOH}$, đây chính là góc cần tìm.

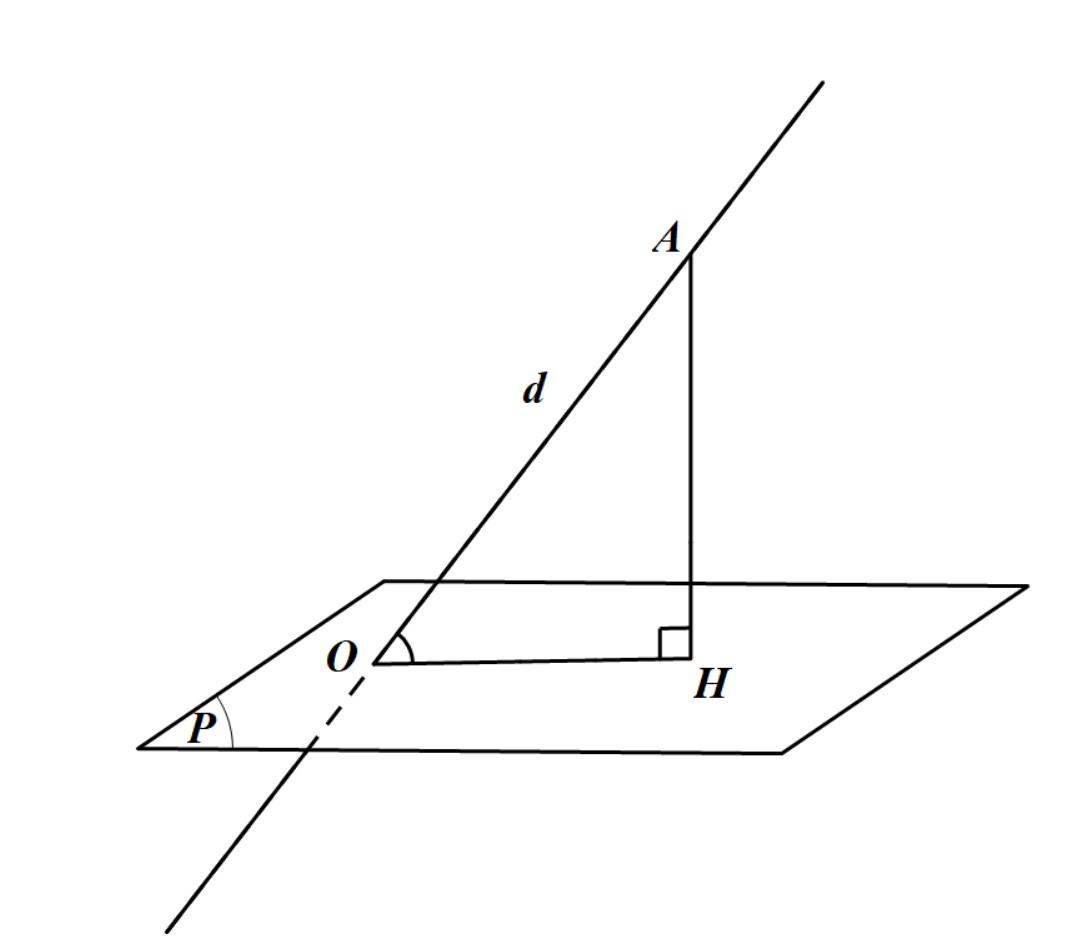
Chú ý. Đối với hình chóp, góc giữa cạnh bên và mặt đáy là góc tạo bởi 3 điểm: đỉnh — điểm chung — chân đường cao hình chóp.

Ví dụ,

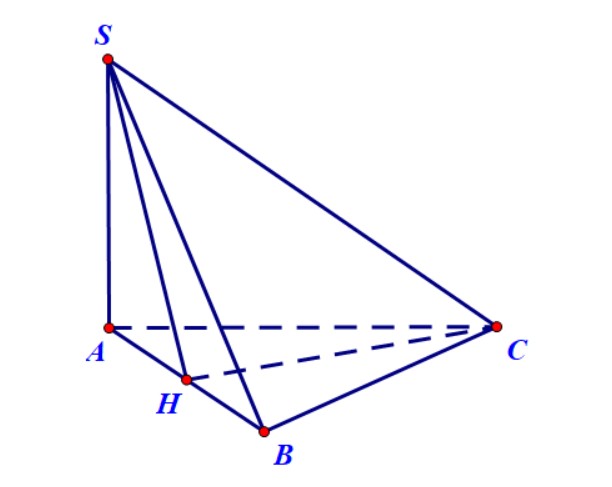
Ví dụ, hình chóp $S.ABC$ có cạnh bên ( SA ) vuông góc với đáy. Hãy xác định góc giữa ( SC) và mặt phẳng ( (ABC) ).

• đỉnh chính là điểm $S$
• điểm chung của cạnh $SC$ và mặt đáy $(ABC)$ chính là điểm $C$
• chân đường cao hình chóp là điểm $A$

Suy ra, góc giữa ( SC) và mặt phẳng ( (ABC) ) là góc ( widehat{SCA} ).

Tương tự, các em cũng có thể dễ dàng tìm được góc giữa cạnh bên $SB$ và mặt đáy $(ABC)$ là ( widehat{SBA} ).

3. Ví dụ tính góc giữa đường thẳng và mặt phẳng

Ví dụ 1. Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình vuông cạnh $ a $. Cạnh $ SA=asqrt{6} $ và vuông góc với đáy $ (ABCD) $. Tính góc giữa:

1. đường thẳng $ SC $ và mặt phẳng $ (ABCD) $;
2. đường thẳng $ SC $ và mặt phẳng $ (SAB) $;
3. đường thẳng $ SB $ và mặt phẳng $ (SAC) $;
4. đường thẳng $ AC $ và mặt phẳng $ (SBC) $.

Hướng dẫn.

1. Để tính góc giữa đường thẳng $ SC $ và mặt phẳng $ (ABCD) $, chúng ta lần lượt thực hiện 3 bước:
   • Giao điểm của đường thẳng $ SC $ và mặt phẳng $ (ABCD) $ là điểm $C$.
   • Trên đường thẳng $SC$, chọn một điểm và xác định hình chiếu vuông góc của nó xuống mặt phẳng $(ABCD)$, ở đây chúng ta chọn điểm $S$ vì dễ thấy hình chiếu vuông góc của $S$ lên mặt phẳng $ (ABCD) $ chính là $A$. (Do giả thiết cạnh $ SA$ và vuông góc với đáy $ (ABCD) $.
   • Như vậy, góc giữa đường thẳng $ SC $ và mặt phẳng $ (ABCD) $ chính là góc $SCA$ và chúng ta đi tính số đo của góc này.
   • Xét tam giác vuông $SAC$ có $ SA=asqrt{6}$ và $AC=asqrt{2}$ (do $AC$ là đường chéo của hình vuông cạnh $a$) nên có [ tan widehat{SCA}=frac{SA}{AC}=frac{asqrt{6}}{asqrt{2}}=sqrt{3} ] Suy ra ( widehat{SCA} = 60^circ ) và đây chính là đáp số cần tìm.
2. Chứng minh được $CB$ vuông góc với $(SAB)$ (em nào chưa làm được thì có thể xem lại bài Cách chứng minh đường thẳng vuông góc với mặt phẳng). Sau đó, làm theo đúng 3 bước trong lý thuyết ta được góc $widehat{CSB}$. Đáp số $arctanfrac{1}{sqrt{7}}$.
3. Gọi $O$ là giao điểm của hai đường chéo $AC,BD$ thì chứng minh được $BO$ vuông góc với $(SAC)$. Góc cần tìm là $widehat{BSO}$. Đáp số $ arcsinfrac{1}{sqrt{14}}$.
4. Trong mặt phẳng $(SAB)$, qua $A$ kẻ đường thẳng vuông góc và cắt $SB$ tại $H$. Chứng minh được $AH$ vuông góc với $(SBC)$ và tìm được góc giữa đường thẳng $ AC $ và mặt phẳng $ (SBC) $ là $widehat{ACH}$. Đáp số $arcsinfrac{sqrt{21}}{7} $.

Ví dụ 2. Cho hình chóp $ S.ABC $ có đáy là tam giác đều cạnh $ a. $ Cạnh bên $ SA $ bằng $ 2a $ và vuông góc với đáy $ (ABC). $

1. Tính góc giữa đường thẳng $ SB $ và mặt phẳng $ (ABC). $
2. Tính góc giữa đường thẳng $ SC $ và mặt phẳng $ (SAB). $
3. Gọi $ M,N $ lần lượt là trung điểm của $ SC $ và $ AC. $
   • Tính góc giữa $ BM $ và mặt phẳng $ (ABC);$
   • Tính góc giữa $ SN $ với mặt phẳng $ (SAB). $

Hướng dẫn.

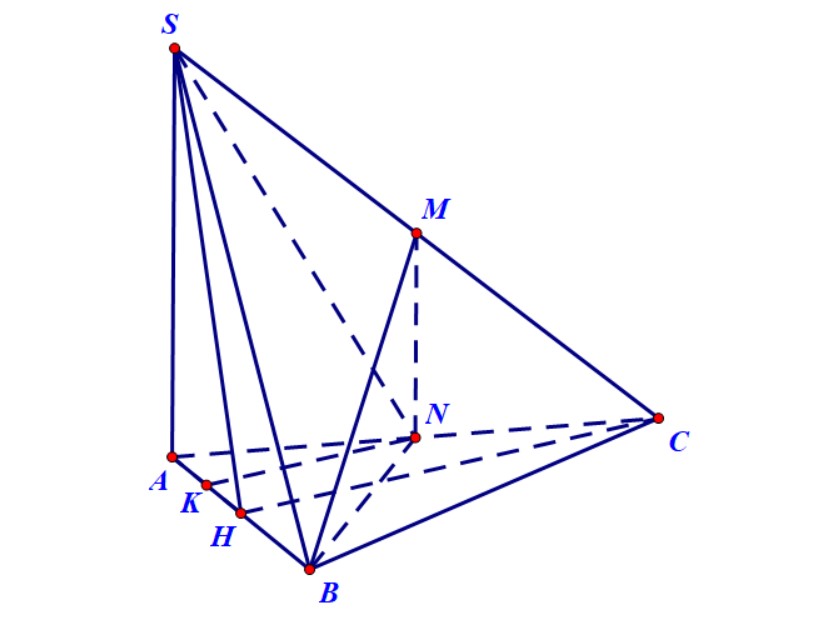
1. Góc giữa đường thẳng $ SB $ và mặt phẳng $ (ABC) $ là góc $widehat{SBA}$.
2. Gọi $H$ là trung điểm $AB$ thì chứng minh được $CH$ vuông góc với $(SAB)$. Góc giữa đường thẳng $ SC $ và mặt phẳng $ (SAB) $ là góc $CSH$.
3. Góc giữa đường thẳng $ BM $ và mặt phẳng $ (ABC)$ là $ widehat{MBN} $có $ tanwidehat{MBN}=frac{2sqrt{3}}{3}$.Trong mặt phẳng $(ABC)$ kẻ $NK$ vuông góc với $AB$ tại $K$ ($NK$ song song với $CH$). Dễ dàng chỉ ra được $NK$ vuông góc với $(SAB)$.Suy ra, góc giữa đường thẳng $ SN $ với mặt phẳng $ (SAB) $ là $ widehat{NSK} $. Tính được $tanwidehat{NSK}=frac{sqrt{3}}{sqrt{17}} $ và suy ra số đo góc cần tìm.

Ví dụ 3. Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a $. Trung tuyến $ SI $ của tam giác đều $ SAB $ vuông góc với đáy $ (ABCD) $ của hình chóp. Chứng minh hai đường thẳng $ SC $ và $ SD $ tạo với mặt phẳng $ (SAB) $ hai góc bằng nhau. Tính góc giữa đường thẳng $ CM $ và mặt phẳng $ (SAB) $, trong đó $ M $ là trung điểm $ SD. $

Hướng dẫn. Hai đường thẳng $ SC $ và $ SD $ cùng tạo với mặt phẳng $ (SAB) $ góc $ 45^circ. $ Hình chiếu của điểm $ C $ lên mặt phẳng $ (SAB) $ là $ B. $ Hình chiếu của điểm $ M $ lên mặt phẳng $ (SAB) $ là trung điểm $ N $ của $ SA. $ Góc giữa đường thẳng $ CM $ và mặt phẳng $ (SAB) $ bằng $ 30^circ. $

Ví dụ 4. Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a $, tâm $ O $ và $ SO $ vuông góc với đáy. Gọi $ M, N $ lần lượt là trung điểm của các cạnh $ SA $ và $ BC $. Biết góc giữa đường thẳng $ MN $ và mặt phẳng $ (ABCD) $ bằng $ 60^circ $. Tính độ dài $ MN $ và $ SO $. Tính góc giữa đường thẳng $ MN $ và mặt phẳng $ (SBD) $.

Hướng dẫn. Gọi $ H $ là trung điểm của $ AO $ thì $ MH $ song song với $ SO $ nên $ H $ là hình chóp vuông góc của $ M $ lên mặt phẳng $(ABCD)$… Đáp số $ MN=frac{asqrt{10}}{2},SO=frac{asqrt{30}}{2};sinleft(MN,(SBD)right)=frac{1}{sqrt{5}} $