Diện tích tam giác là môn toán lớp 1 các em sẽ được học. Nhưng vì trong tam giác có nhiều hạng tử khác nhau nên số lượng căn thức cũng sẽ nhiều hơn. Vì vậy, để giúp các em học và ghi nhớ kiến thức này một cách hiệu quả, mời các em cùng manta.edu.vn tham khảo bài viết dưới đây.
Công thức tính diện tích tam giác
Với hình tam giác , tùy vào hình dạng sẽ sử dụng các công thức khác nhau. Dưới đây là một số công thức thông dụng, dễ hiểu và được sử dụng nhiều nhất để bạn tham khảo và áp dụng:
Tính diện tích tam giác thường
Cho tam giác thường ABC có 3 cạnh a, b, c và ha là đường cao của đỉnh a. Chúng ta có:
Diện tích của tam giác bằng ½ tích của chiều cao kẻ từ đỉnh đến độ dài cạnh đối diện của đỉnh đó.
S = (axh)/2
Công thức dẫn xuất:
h = (S x 2)/a hoặc a = (S x 2)/h
Ví dụ:
Tính diện tích tam giác có cạnh đáy là 5m, chiều cao là 24dm.
Bài giải: Chiều cao 24dm = 2,4m
Diện tích của tam giác là
S=(5 x 2,4)/2 = 6m2
Tính diện tích tam giác cân
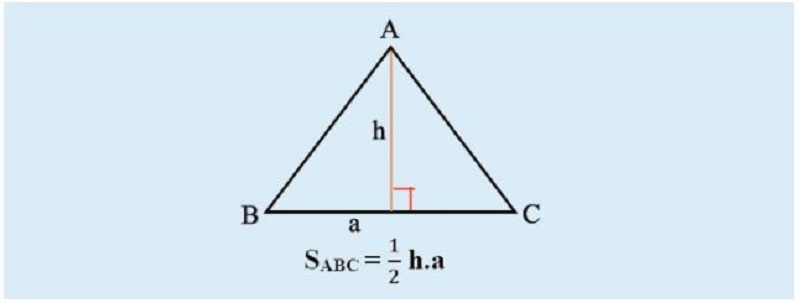
Tam giác cân là tam giác có hai cạnh bằng nhau . Diện tích của một tam giác cân bằng tích của chiều cao nối từ đỉnh của tam giác đến đáy của tam giác, rồi chia cho 2.
Công thức tính diện tích tam giác cân:
S = (axh)/2
- a: Độ dài đáy của tam giác cân (đáy là một trong ba cạnh của tam giác)
- h: Chiều cao của tam giác (chiều cao của tam giác bằng đoạn thẳng kẻ từ đỉnh xuống đáy).
Ví dụ: Tính diện tích tam giác cân có:
a, Độ dài cạnh đáy là 6cm, chiều cao là 7cm
b, Độ dài cạnh đáy là 5m, chiều cao là 3,2m
Câu trả lời:
a) Diện tích tam giác là:
(6 x 7) : 2 = 21 (cm2)
Đáp số: 21cm2
b, Diện tích tam giác là:
(5 x 3,2) : 2 = 8 (m2)
Đáp số: 8m2
Tính diện tích tam giác đều
Tam giác đều là tam giác có 3 cạnh bằng nhau. Cụ thể, cách tính diện tích tam giác đều sẽ giống như tính diện tích tam giác thường, khi ta chỉ cần biết cạnh đáy và chiều cao của tam giác.
Vậy diện tích của tam giác đều sẽ bằng tích của chiều cao với đáy, khi đó không cho 2.
Công thức tính diện tích tam giác đều:
S = (axh)/2
- a: Độ dài đáy của tam giác đều (đáy là một trong ba cạnh của tam giác)
- h: Chiều cao của tam giác (chiều cao của tam giác bằng đoạn thẳng kẻ từ đỉnh xuống đáy).
Ví dụ: Tính diện tích tam giác đều có:
a, Độ dài một cạnh của tam giác là 6 cm và chiều cao là 10 cm
b, Độ dài một cạnh của tam giác là 4cm và chiều cao là 5cm
Câu trả lời
a, Diện tích tam giác là:
(6 x 10) : 2 = 30 (cm2)
Đáp số: 30cm2
b, Diện tích tam giác là:
(4 x 5) : 2 = 10 (cm2)
Đáp số: 10cm2
Tính diện tích tam giác vuông
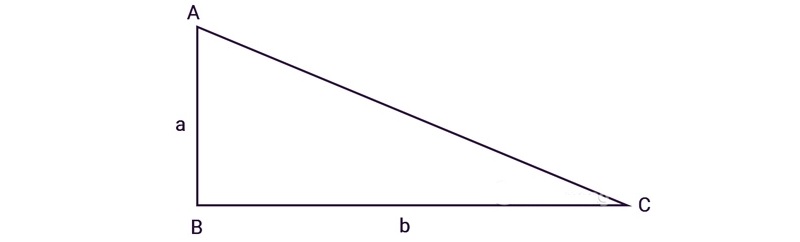
Tam giác vuông là tam giác có một góc vuông bằng 90° . Về cách tính diện tích tam giác vuông cũng sẽ bằng ½ tích chiều cao với độ dài đáy. Nhưng với loại hình tam giác này sẽ hơi khác một chút vì đã thể hiện rõ độ dài và chiều cao của đáy nên các bạn không cần vẽ thêm để tính chiều cao của hình.
Công thức tính diện tích tam giác vuông: S = (a X h) / 2
Nhưng vì một tam giác vuông có 2 cạnh góc vuông nên chiều cao sẽ tương ứng với 1 cạnh góc vuông, kéo theo đó là độ dài đáy sẽ tương ứng với cạnh góc vuông còn lại.
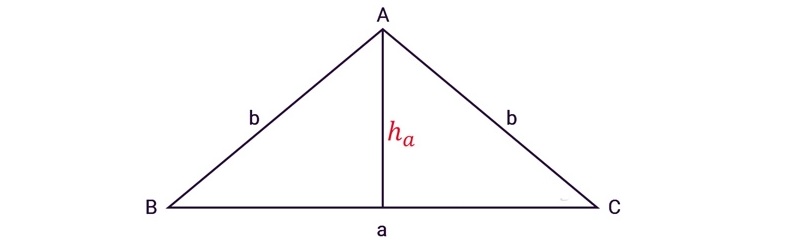
Từ đó ta có công thức tính diện tích tam giác vuông:
S = (axb)/2
Trong đó a, b là độ dài hai cạnh góc vuông
Công thức dẫn xuất:
a = (S x 2) : b hoặc b = (S x 2): a
Ví dụ: Tính diện tích tam giác vuông có:
a, Hai cạnh của góc vuông là 3cm và 4cm . tương ứng
b, Hai cạnh góc vuông là 6m và 8m . tương ứng
Câu trả lời:
a) Diện tích tam giác là:
(3 x 4) : 2 = 6 (cm2)
Đáp số: 6cm2
b, Diện tích tam giác là:
(6 x 8) : 2 = 24 (m2)
Đáp số: 24m2
Tính diện tích tam giác cân
Tam giác vuông cân là tam giác vừa vuông cân. Như hình vẽ, cho tam giác ABC vuông tại A, a là độ dài hai cạnh của góc vuông.
Dựa vào công thức tính tam giác vuông cho tam giác vuông cân, có cùng chiều cao và cạnh đáy. Ta có công thức:
S = 1/2 x 2
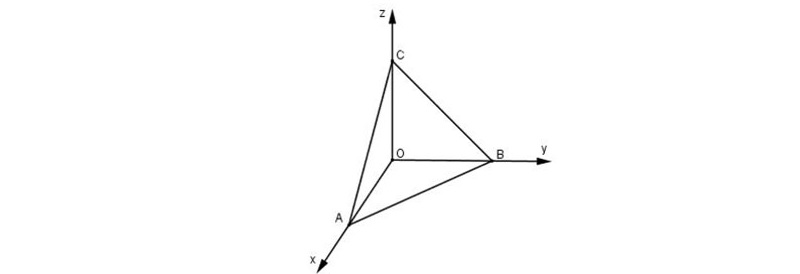
Công thức tính diện tích tam giác trong hệ tọa độ Oxyz
Về mặt lý thuyết, chúng ta có thể sử dụng các công thức phẳng lượng giác cho tam giác trong không gian Oxyz. Nhưng điều đó sẽ khó tính toán. Vậy trong không gian Oxyz ta sẽ tính diện tích tam giác dựa vào tích có hướng.
Trong không gian Oxyz, cho tam giác ABC. Diện tích tam giác ABC được tính theo công thức:
Hình minh họa:
Trong không gian Oxyz, cho tam giác ABC có tọa độ ba đỉnh lần lượt là A(-1;1;2), B(1;2;3), C(3;-2,0). Tính diện tích tam giác ABC.
Dung dịch:
Các dạng bài tập tính diện tích tam giác từ cơ bản đến nâng cao
Đối với kiến thức về tam giác tùy theo từng khối lớp sẽ có những bài tập riêng. Nhưng đối với các em học sinh tiểu học, các em sẽ thường gặp các dạng bài tập tính diện tích tam giác sau:
Dạng 1: Tính diện tích tam giác khi biết độ dài đáy và chiều cao
Đối với dạng bài tập này, thông thường đề bài sẽ cho thông tin về chiều cao và độ dài của cạnh đáy. Vậy bạn chỉ cần áp dụng công thức tính chu vi tam giác thường là tìm được đáp án chính xác.
Ví dụ: Tính diện tích tam giác đều và tam giác vuông với:
a) Chiều dài đáy là 32 cm và chiều cao là 25 cm.
b) Hai cạnh góc vuông lần lượt là 3dm và 4dm.
Câu trả lời:
a) Diện tích tam giác là:
32 x 25 : 2 = 400 (cm2)
b) Diện tích tam giác là:
3 x 4 : 2 = 6 (dm2)
Đáp số: a) 400cm2; b) 6dm2
Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao
Ở dạng bài tập này, dữ liệu bài toán sẽ cho biết các thông số về chiều cao, diện tích của tam giác, yêu cầu học sinh tính độ dài cạnh đáy. Vậy từ công thức tính diện tích ta suy ra công thức tính độ dài đáy: a = S x 2 : h
Ví dụ: Cho hình tam giác có diện tích 4800cm2, chiều cao 80cm. Chiều dài của cạnh cơ sở là bao nhiêu?
Câu trả lời:
Độ dài cạnh đáy của tam giác là:
4800 x 2 : 80 = 120 (cm)
Đáp số: 120cm
Dạng 3: Tính chiều cao khi biết diện tích và độ dài đáy
Cũng từ công thức tính diện tích tam giác ta cũng sẽ suy ra công thức tính chiều cao của hình như sau: h = S x 2 : a
Ví dụ: Cho tam giác biết diện tích là 1125cm2, độ dài đáy là 50cm, hãy tính chiều cao của tam giác đó.
Câu trả lời:
Chiều cao của tam giác là:
1125 x 2 : 50 = 45 (cm)
Đáp số: 45cm
Bài tập toán tính diện tích tam giác cho bé luyện tập
Dựa vào những kiến thức trên, sau đây là một số bài tập tính diện tích hình vuông để các em luyện tập:
Bí quyết giúp bé học và ghi nhớ kiến thức diện tích tam giác hiệu quả
Đối với những kiến thức liên quan đến diện tích tam giác sẽ có nhiều dạng bài phức tạp, cũng như nhiều nội dung cần học. Để giúp trẻ tiếp thu kiến thức một cách hiệu quả, dưới đây là một số bí quyết cha mẹ có thể tham khảo:
Nắm vững kiến thức cơ bản về diện tích tam giác
Cha mẹ nên thường xuyên kiểm tra kiến thức riêng về môn học hay diện tích tam giác để biết năng lực học tập của con đến đâu. Cụ thể, hãy thử đặt câu hỏi liên quan đến công thức tính diện tích tam giác bất kỳ, xem bài làm của con bạn, v.v.
Qua đây sẽ giúp bạn biết được sức học của con mình như thế nào, con còn yếu những phần nào để tiến hành hướng dẫn, củng cố kịp thời.
Luôn luyện tập cùng bé
Học đi đôi với hành là yếu tố không thể thiếu. Cách thực hành ở đây là cùng con làm các bài tập trong sách giáo khoa, tìm hiểu thêm các dạng bài tập khác nhau về diện tích tam giác, làm các bài kiểm tra thử, tổ chức các trò chơi học toán, tổ chức các cuộc thi nhỏ cho con tham gia,…
Vì được luyện tập thường xuyên, trẻ sẽ dễ dàng ghi nhớ những kiến thức đã học, biết cách vận dụng vào thực tế và đặc biệt là hình thành tư duy sáng tạo trong quá trình học hiệu quả hơn.
Phần kết luận
Trên đây là tổng hợp đáp án về kiến thức diện tích tam giác . Đây cũng là một dạng toán khá khó và quan trọng trong quá trình học của các bé. Vì vậy, phụ huynh hãy cùng con tham khảo và tiến hành ôn tập để giúp nâng cao hiệu quả học tập của con tốt hơn.
