Tích vô hướng và tích có hướng của hai vectơ và cách giải – Toán lớp 12
I. LÝ THUYẾT
1. Tích vô hướng của hai vectơ
a) Tích vô hướng của hai vectơ
Trong không gian Oxyz, tích vô hướng của hai vectơ a→=a1; a2; a3và b→=b1; b2; b3 được xác định bởi công thức:
a→.b→=a1b1+a2b2+a3b3
b) Ứng dụng của tích vô hướng
+ Cho vectơ a→=a1; a2; a3, khi đó độ dài của vectơ a→ được tính theo công thức:
a→= a12+a22+a22
+ Cho hai điểm AxA; yA; zA và BxB; yB; zB. Khi đó khoảng cách giữa hai điểm A, B chính là độ dài của vectơ AB→. Do đó ta có
+ Cho vectơ a→=a1; a2; a3 và b→=b1; b2; b3. Khi đó góc giữa hai vectơ a→ và b→ được tính theo công thức:
cos(a→, b→) = a→.b→a→.b→ = a1b1+a2b2+a3b3a12+a22+a32.b12+b22+b32
(với a→, b→≠0→)
+ Hai vectơ vuông góc: Cho vectơ a→=a1; a2; a3 và b→=b1; b2; b3. Khi đó:
a→⊥b→ ⇔ a→.b→=0 ⇔a1b1+a2b2+a3b3=0
2. Tích có hướng của hai vectơ
a) Tích có hướng của hai vectơ
Trong không gian Oxyz cho hai vectơ a→=(a1;a2;a3), b→=(b1; b2; b3). Tích có hướng của hai vectơ a→ và b→, kí hiệu là a→,b→, được xác định bởi
a→,b→ = a2a3b2b3 ; a3a1b3b1 ; a1a2b1b2=a2b3−a3b2;a3b1−a1b3;a1b2−a2b1
Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.
b) Tính chất của tích có hướng:

Từ đó suy ra 4 điểm A, B, C, D là 4 đỉnh của một tứ diện khi 3 vectơ AB→; AC→; AD→ không đồng phẳng hay AB→,AC→.AD→≠0 và 4 điểm A, B, C, D đồng phẳng khi AB→,AC→.AD→=0.
3. Ứng dụng của tích có hướng

II. PHƯƠNG PHÁP GIẢI VÀ VÍ DỤ MINH HỌA
1. Tích vô hướng của hai vectơ
Dạng 1: Tính biểu thức tọa độ tích vô hướng
Phương pháp giải:
Cho hai vectơ a→=a1; a2; a3 và b→=b1; b2; b3, khi đó: a→.b→=a1b1+a2b2+a3b3
Ví dụ 1: Trong không gian Oxyz, cho u→=−1;3;2, v→=−3;−1;2. Khi đó u→.v→ bằng
A. 10
B. 2
C. 3
D. 4
Hướng dẫn giải
u→.v→=−1.−3+3.−1+2.2=3−3+4=4
Chọn D.
Dạng 2: Tính độ dài của một vectơ
Phương pháp giải: Cho vectơ a→=a1; a2; a3, khi đó độ dài của vectơ a→ được tính theo công thức:
a→= a12+a22+a22
Ví dụ 2: Trong không gian Oxyz cho vectơ a→=2; 4; 1. Độ dài vectơ a→ là
A. 21
B. 7
C. 21
D. 7
Hướng dẫn giải:
Độ dài vectơ a→ là:
a→= 22+42+12=21
Chọn A.
Dạng 3: Khoảng cách giữa hai điểm
Phương pháp giải: Cho hai điểm AxA; yA; zA và BxB; yB; zB. Khi đó khoảng cách giữa hai điểm A, B chính là độ dài của vectơ AB→. Do đó ta có
Ví dụ 3: Trong không gian với hệ tọa độ Oxyz, cho điểm A (1; 2; 3), trên trục Oz lấy điểm M sao cho AM=5. Tọa độ của điểm M là
A. M (0; 0; 3).
B. M (0; 0; 2).
C. M (0; 0; -3).
D. M (0; 3; 0).
Hướng dẫn giải
Do M∈Oz⇒M (0; 0; m)
AM=0−12+0−22+m−32=(m−3)2+5
Mặt khác AM=5 nên
(m−3)2+5=5⇔m−32+5=5
⇔m – 3 = 0 ⇔m = 3
Suy ra M (0; 0; 3).
Chọn A.
Dạng 4: Góc giữa hai vectơ
Phương pháp giải: Cho vectơ a→=a1; a2; a3 và b→=b1; b2; b3. Khi đó góc giữa hai vectơ a→ và b→ được tính theo công thức:
cos(a→, b→) = a→.b→a→.b→ = a1b1+a2b2+a3b3a12+a22+a32.b12+b22+b32
(với a→, b→≠0→)
Ví dụ 4: Trong không gian Oxyz, cho bốn điểm A (1; 0; 0), B (0; 1; 0), C (0; 0; 1) và D (-2; 1; -1). Tính góc giữa hai vectơ AB→ và CD→.
A. 450
B. 600
C. 900
D. 1350
Hướng dẫn giải
Gọi φ là góc tạo bởi hai vectơ AB→ và CD→.
Ta có:
AB→=−1;1;0, CD→=−2;1;−2
Khi đó:
cosφ=cosAB→,CD→=−1.−2+1.1+0.−2−12+12+02.−22+12+−22=12⇒φ=450
Chọn A.
Dạng 5: Tìm điều kiện để hai vectơ vuông góc
Phương pháp giải: Cho vectơ a→=a1; a2; a3 và b→=b1; b2; b3. Khi đó:
a→⊥b→ ⇔ a→.b→=0 ⇔a1b1+a2b2+a3b3=0
Ví dụ 5: Trong không gian với hệ tọa độ Oxyz, cho các vec tơa→=−1;1;0,b→=1;1;0 và c→=1;1;1. Mệnh đề nào dưới đây sai?
A. c→⊥b→
B. c→=3
C. a→⊥b→
D. a→=2
Hướng dẫn giải

Chọn A.
2. Tích có hướng của hai vectơ
Tích có hướng của hai vectơ thường sử dụng để tính diện tích tam giác; tính thể tích khối tứ diện, thể tích hình hộp; chứng minh các vectơ đồng phẳng – không đồng phẳng, chứng minh các vectơ cùng phương.
Dạng 1: Tính tích có hướng của hai vectơ
Phương pháp giải: Cho hai vectơ a→=a1; a2; a3 và b→=b1; b2; b3, khi đó:
a→,b→ = a2a3b2b3 ; a3a1b3b1 ; a1a2b1b2=a2b3−a3b2;a3b1−a1b3;a1b2−a2b1
Ví dụ 1: Trong không gian với hệ trục tọa độ Oxyz, cho a→=3;2;1, b→=3;2;5. Khi đó a→,b→ có tọa độ bằng
A. 8;−12;5
B. 8;−12;0
C. 0;8;12
D. 0;8;−12
Hướng dẫn giải
a→=3;2;1b→=3;2;5⇒a→,b→=2.5−2.1; 1.3−3.5; 3.2−3.2=8; −12; 0
Chọn B.
Dạng 2: Tìm điều kiện để ba vectơ đồng phẳng
Phương pháp giải: a→, b→ và c→ đồng phẳng [a→, b→] .c→=0
Ví dụ 2: Trong không gian với hệ tọa độ Oxyz cho vectơ a→=1;m;2; b→=m+1;2;1; c→=0;m−2;2. Giá trị của m để a→, b→, c→ đồng phẳng là
A. 25
B. −25
C. 15
D. 1.
Hướng dẫn giải
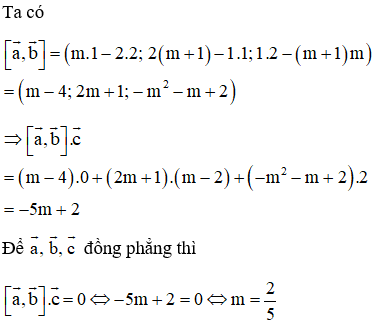
Chọn A.
Dạng 3: Tính diện tích một số hình phẳng
Phương pháp giải:
Áp dụng các công thức sau:
+) Diện tích hình bình hành ABCD:
SABCD=AB→,AD→
+) Diện tích tam giác ABC:
SABC=12AB→, AC→
Ví dụ 3: Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC với A (1; 2; 1), B (2; 1; 3) và C (3; 2; 2). Diện tích tam giác ABC bằng
A. 112
B. 3
C. 132
D. 142
Hướng dẫn giải
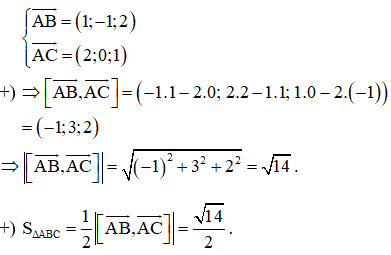
Chọn D.
Dạng 4: Tính thể tích khối hộp và tứ diện
Phương pháp giải:
Áp dụng các công thức sau:
+) Thể tích khối hộp ABCD. A’B’C’D’:
VABCD.A’B’C’D’ = [AB→, AD→].AA’→
+) Thể tích tứ diện ABCD:
VABCD=16[AB→, AC→] .AD→
Ví dụ 4: Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD với A (1; 2; 1), B (2; 1; 3), C (3; 2; 2), D (1; 1; 1). Thể tích của tứ diện ABCD bằng
A. 1
B. 2
C. 12
D. 3.
Hướng dẫn giải
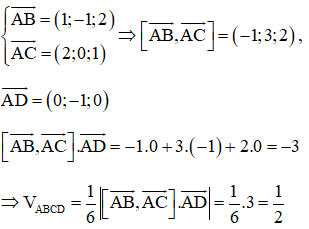
Chọn C.
III. BÀI TẬP ÁP DỤNG
Câu 1: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1; 0; -2), B (2; 1; -1). Độ dài của đoạn thẳng AB là
A. 2
B. 18
C. 27
D. 3
Câu 2: Trong không gian với hệ trục tọa độ Oxyz, cho hai vectơ a→=1; −2; 0 và b→=−2; 3;1. Khẳng định nào sau đây là sai?
A. a→.b→=−8
B. a→+b→=−1; 1; −1
C. b→=14
D. 2a→=2; −4; 0
Câu 3: Trong không gian với hệ tọa độ Oxyz, cho hai vectơ a→=2;4;−2 và b→=3;−1;6. TínhP=a→.b→.
A. P = -10
B. P = -40
C. P = 16
D. P = -34
Câu 4: Trong không gian với hệ trục tọa độ Oxyz, cho hai vectơ a→=2;1;0 vàb→=−1;0;−2. Tính cosa→,b→.
A. cosa→,b→=−225
B. cosa→,b→=−25
C. cosa→,b→=225
D. cosa→,b→=25
Câu 5: Trong không gian với hệ trục tọa độ Oxyz, cho a→=1;−2;1,b→=2;−4;2. Khi đó a→,b→ có tọa độ bằng
A. (0 ; 0 ; 0).
B. (1 ; 1 ; 1)
C. (2 ; 8 ; 2)
D. (1 ; -2 ; 1).
Câu 6: Cho bốn véc tơ a→=−1;1;0,b→=1;1;0 ,c→=1;1;1, d→=2;0;1. Chọn mệnh đề đúng.
A.a→, b→, c→ đồng phẳng.
B. a→, b→, d→ đồng phẳng.
C. a→, c→, d→ đồng phẳng.
D. d→, b→, c→ đồng phẳng.
Câu 7: Trong không gian với hệ tọa độ Oxyz cho tam giác ABC biết A (1; 1; 1), B (4; 3; 2), C (5; 2; 1). Diện tích tam giác ABC là
A. 424
B. 42
C. 242
D. 422
Câu 8: Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD có A (1; 0; 1), B (2; 0; -1), C (0; 1; 3), D (3; 1; 1). Thể tích khối tứ diện ABCD là
A.V=23
B. V=43
C. V = 4
D. V = 2.
Câu 9: Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD. A’B’C’D’ có A (-1; 0; 2), B (1; 1; -1), D (0; 1; 1), A’ (2; -1; 0). Thể tích V của khối hình hộp ABCD. A’B’C’D’ là
A. V = 1.
B. V = 4.
C. V = 5.
D. V = 6.
Câu 10: Cho ba vectơ a→=4;2;5,b→=3;1;3,c→=2;0;1. Chọn mệnh đề đúng:
A. Ba vectơ đồng phẳng
B. Ba vectơ không đồng phẳng.
C. Ba vectơ cùng phương
D. c→=a→,b→
ĐÁP ÁN
