Trong bài viết này, HocThatGioi sẽ chia sẻ đến các bạn phương pháp tính khoảng cách giữa 2 đường thẳng trong không gian. Đây là dạng bài cơ bản thường xuất hiện trong các đề thi và là cơ sở để giải những bài toán nâng cao hơn. Bài viết này sẽ giúp các bạn nắm vững kiến thức về dạng này và tự tin hơn khi đối mặt với nó. Cùng bắt đầu bài học ngay nhé!
1. Khoảng cách giữa 2 đường thẳng trong không gian là gì?
Khoảng cách giữa 2 đường thẳng chéo nhau là độ dài đoạn vuông góc chung của 2 đường thẳng đó. Khoảng cách giữa 2 đường thẳng song song được tính đơn giản bằng khoảng cách từ 1 điểm của đường này đến đường còn lại. (Cũng là đoạn vuông góc chung của 2 đường thẳng song song).
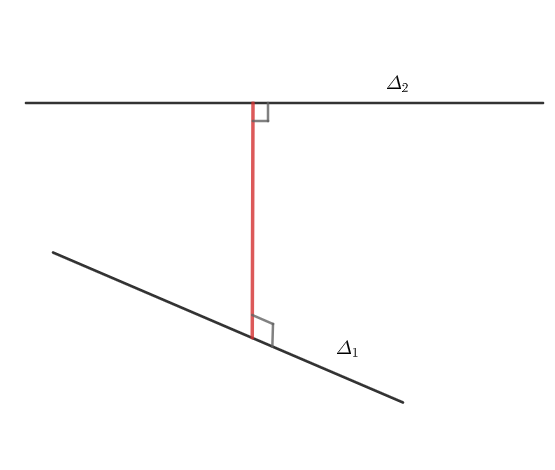
Khoảng cách giữa 2 đường thẳng chéo nhau còn có thể nói là khoảng cách giữa một đường với mặt phẳng song song với đường đó và chứa đường còn lại.
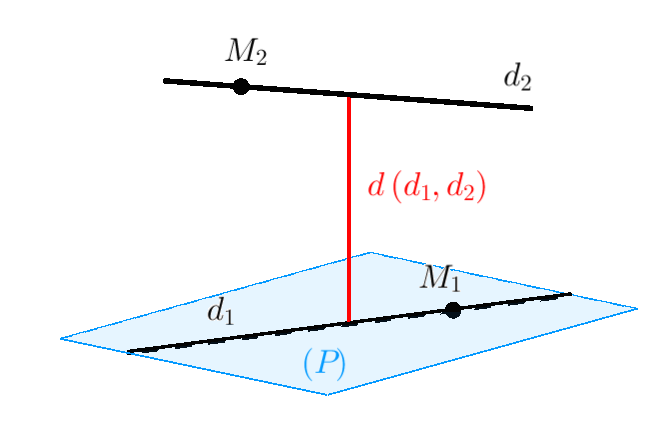
Khoảng cách giữa 2 đường thẳng chéo nhau còn có thể nói là khoảng cách giữa 2 mặt phẳng song song chứa 2 đường thẳng đó.
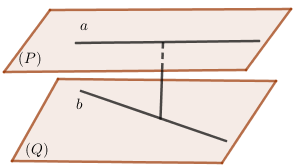
Kí hiệu: d(a,b) khoảng cách giữa 2 đường thẳng a và b.
2. Cách tính khoảng cách giữa 2 đường thẳng trong không gian
Giữa 2 đường thẳng có vị trí khác nhau thì sẽ có các cách tính phù hợp.
2.1 Khoảng cách giữa 2 đường thẳng song song
Để tính khoảng cách giữa 2 đường thẳng song song, ta có thể làm 1 trong 2 cách sau:
Cách 1: Lấy một điểm bất kì trên đường thẳng này, sau đó tính khoảng cách từ điểm đó đến đường thẳng kia.
==> Tham khảo ngay bài viết Cách tìm khoảng cách từ 1 điểm đến 1 đường thẳng trong không gian nếu bạn còn chưa nắm rõ cách tính nhé!
Cách 2: Giả sử có hai đường thẳng d_1 và d_2 song song với nhau có phương trình lần lượt là:
- d_1:left{begin{matrix} x=x_1+at \ y=y_1+bt \ z=z_1+ct end{matrix}right.
- d_2:left{begin{matrix} x=x_2+kat \ y=y_2+kbt \ z=z_2+kct end{matrix}right.
Khi đó, khoảng cách giữa 2 đường thẳng này sẽ được tính bằng công thức:
2.2 Khoảng cách giữa 2 đường thẳng chéo nhau
Giả sử có hai đường thẳng d_1 và d_2 chéo nhau có phương trình lần lượt là:
- d_1:left{begin{matrix} x=x_1+a_1t \ y=y_1+b_1t \ z=z_1+c_1t end{matrix}right.
- d_2:left{begin{matrix} x=x_2+a_2t \ y=y_2+b_2t \ z=z_2+c_2t end{matrix}right.
Khi đó, khoảng cách giữa 2 đường thẳng này sẽ được tính bằng công thức:
Lưu ý: Để sử dụng công thức này, trước tiên ta cần phải xét xem chúng có song song hay trùng nhau hay không. Vì nếu song song hay trùng nhau thì mẫu số sẽ bằng 0. Còn nếu kết quả ra 0 thì 2 đường thẳng đó cắt nhau => Khoảng cách là 0.
Xem ví dụ dưới đây:
3. Bài tập khoảng cách giữa 2 đường thẳng
Thử sức ngay với những bài tập dưới đây để ôn luyện lại kiến thức ở trên nhé!
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Cách tính khoảng cách giữa 2 đường thẳng trong không gian Oxyz. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi. Đừng quên để lại 1 like, 1 cmt dể tạo động lực cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!
Bài viết khác liên quan đến Lớp 12 – Toán – Phương trình đường thẳng trong không gian
- Phương trình đường thẳng, mặt phẳng và mặt cầu trong không gian Oxyz hay chi tiết nhất
- Phương trình đường thẳng trong không gian Oxyz – Góc và khoảng cách giữa đường thẳng
- Cách viết phương trình đường thẳng trong không gian Oxyz – bài tập áp dụng
- Hình chiếu vuông góc của điểm lên đường thẳng lên mặt phẳng trong không gian Oxyz
- Quan hệ vuông góc và song song của đường thẳng, mặt phẳng trong không gian
- Vị trí tương đối của đường thẳng và mặt phẳng trong không gian siêu chi tiết.
- Góc giữa đường thẳng và mặt phẳng cực chi tiết và dễ hiểu.
- Cách tính khoảng cách từ 1 điểm đến 1 đường thẳng trong không gian Oxyz-bài tập áp dụng
- Cách tính góc giữa 2 đường thẳng trong không gian Oxyz – bài tập áp dụng
- Cách tính góc giữa đường thẳng và mặt phẳng trong không gian Oxyz – bài tập áp dụng
- Vị trí tương đối của đường thẳng và mặt phẳng với mặt cầu trong không gian Oxyz
- Vị trí tương đối của hai đường thẳng trong không gian siêu dễ.
