Hình học luôn là những bài toán hay và hóc búa. Để có thể giải được cái bài toán hình thì người học cần phải nắm chắc kiến thức lý thuyết. Trong hình học không gian, khái niệm về tứ giác nội tiếp và các kiến thức liên quan về khái niệm này luôn là đề bài khó. Vì thế, làm cách nào để người học có thể vận dụng tốt nhất và giải được các bài về lĩnh vực này. Hãy theo dõi ngay bài viết dưới đây, ReviewAZ sẽ hướng dẫn bạn cách chứng minh tứ giác nội tiếp đơn giản nhất.
Tứ giác nội tiếp là gì?
Đầu tiên để có thể chứng minh tứ giác nội tiếp, bạn cần hiểu tứ giác nội tiếp là gì. Tứ giác là hình có 4 cạnh và được minh họa bởi 4 điểm khác nhau không thuộc cùng một đường thẳng.
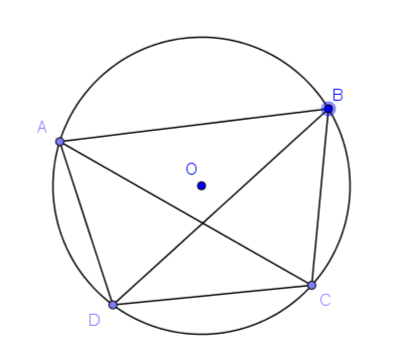
Trong một hình học phẳng, một tứ giác được gọi là tứ giác nội tiếp khi có 4 đỉnh đều thuộc đường tròn đó. Đường tròn có 4 điểm trên được gọi là đường tròn ngoại tiếp hình tứ giác, còn các đỉnh của tứ giác thì được gọi là đồng viên. Bên cạnh đó, tâm đường tròn được gọi là tâm đường tròn ngoại tiếp hình tứ giác, và bán kính đường tròn ngoại tiếp hình tứ giác.
Định lý: Trong tứ giác nội tiếp đường tròn, hai góc đối diện nhau sẽ có tổng bằng 180 độ
Định lý đảo: Nếu trong một tứ giác có hai góc đối diện nhau có tổng bằng 180 độ thì tứ giác đó nội tiếp đường tròn.
Một số hệ quả của tứ giác nội tiếp:
- Hai góc nội tiếp đường tròn đều chắn một cung thì bằng nhau.
- Góc nội tiếp bằng ½ góc ở tâm khi chúng cùng chắn một cung.
- Góc tạo bởi tiếp tuyến và dây cung sẽ bằng góc nội tiếp cùng chắn một cung.
Thông thường, các tứ giác nội tiếp thường là các tứ giác lồi. Tuy nhiên, trong một vài trường hợp, các tứ giác nội tiếp cũng có nhiều tứ giác lõm. Lưu ý rằng, bất kỳ tam giác nào cũng có đường tròn ngoại tiếp; song, không phải tứ giác nào cũng được gọi là tứ giác nội tiếp.
Có thể bạn quan tâm: Cách tính diện tích hình thang giúp cho việc học tập trở nên thuận lợi
Các cách chứng minh tứ giác nội tiếp
Ở phần trên, chúng tôi đã hướng dẫn cho bạn nhận biết một tứ giác nội tiếp là tứ giác như thế nào. Đồng thời cũng có khẳng định rằng, không phải tứ giác nào cũng có đường tròn ngoại tiếp. Chính vì thế, để chắc chắn rằng tứ giác có nội tiếp đường tròn hay không, chúng ta cần phải chứng minh cho chúng. Cũng lưu ý, các tứ giác nội tiếp đường tròn trong bài viết đều là tứ giác lồi.
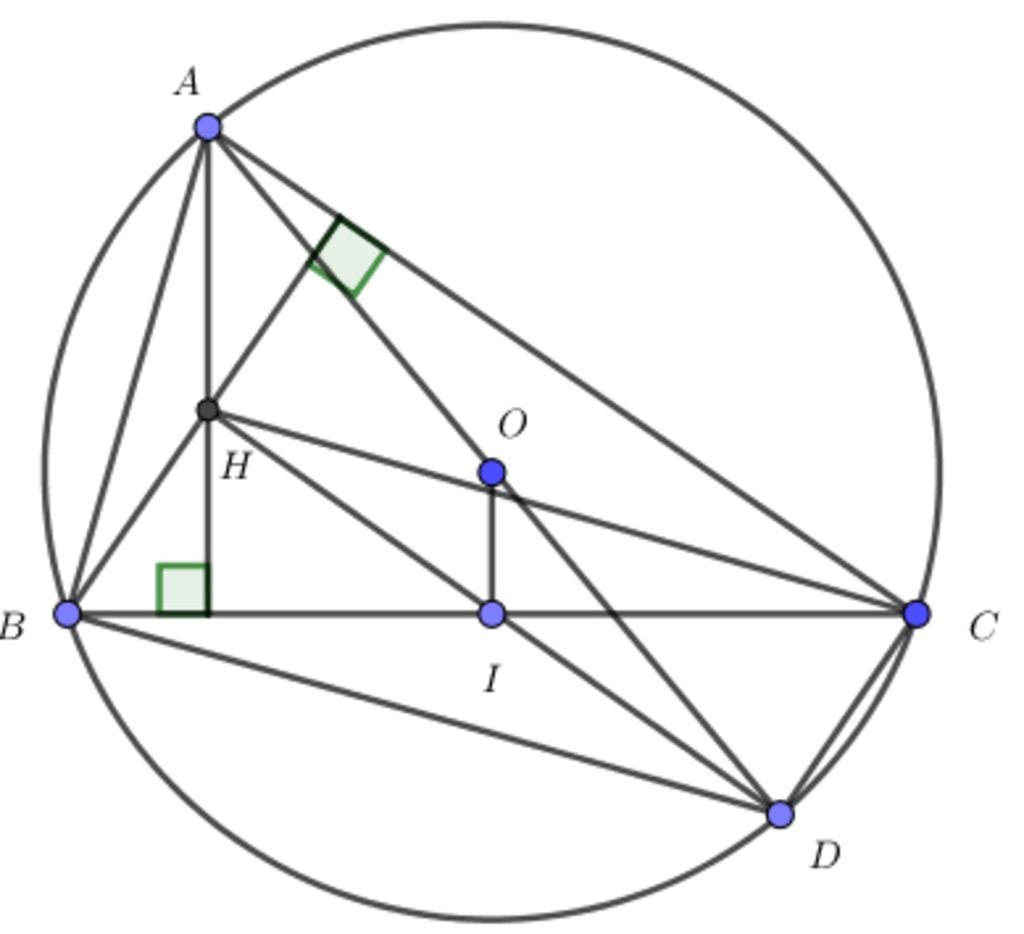
Phương pháp 1: Chứng minh hai góc đối nhau có tổng bằng 180 độ
Trong phần định lý của tứ giác nội tiếp đã nói rằng: hai góc đối nhau sẽ có tổng bằng 180 độ. Chính vì thế, để chứng minh một tứ giác nội tiếp đường tròn, chúng ta có thể sử dụng định lý này.
Ta có: Nếu tứ giác ABCD có tổng hai góc đối nhau trong tam giác bằng 180 độ thì ta gọi tứ giác ABCD là tứ giác nội tiếp.
Chứng minh:
Nếu góc BAD = góc BCD = 90 độ thì tứ giác ABCD là tứ giác nội tiếp đường tròn tâm O đường kính BD.
Nếu tổng của hai góc kề bù nhau trong tam giác là góc EAD = góc BCD thì tứ giác ABCD cũng được gọi là tứ giác nội tiếp đường tròn tâm O, đường kính BD.
Phương pháp 2: Chứng minh tứ giác có góc ngoài của một đỉnh bằng góc trong của đỉnh đối diện
Ta có: tứ giác ABCD có góc ngoài của đỉnh A bằng góc trong của đỉnh C (trường hợp đỉnh A và đỉnh C là hai đỉnh đối nhau). Như vậy, có thể kết luận rằng, tứ giác ABCD là tứ giác nội tiếp đường tròn tâm O đường kính BD.
Chứng minh:
Theo định lý, tứ giác có hai đỉnh đối nhau bằng 180 độ thì tứ giác đó là tứ giác nội tiếp. Như vậy, nếu góc ở đỉnh A và góc của đỉnh C bằng 180 độ thì góc ngoài của đỉnh A sẽ bằng góc ở đỉnh C (vì góc đỉnh A và góc ngoài đỉnh A là hai góc kề bù).
Phương pháp 3: Chứng minh rằng hai đỉnh cùng kề một cạnh và cùng nhìn cạnh đó dưới hai góc bằng nhau 90 độ
Ta có: Cho tứ giác ABCD và các dữ liệu bài cho, học sinh chứng minh được góc DAC và DBC cùng nhìn cạnh CD dưới một góc 90 độ. Từ đó, học sinh có thể khẳng định rằng, tứ giác ABCD là tứ giác nội tiếp đường tròn tâm O, đường kính CD.
Phương pháp 4: Chứng minh 4 điểm của tứ giác đều cách một điểm cố định một khoảng bằng nhau
Nếu đề bài cho chúng ta một đường tròn tâm O có bán kính R, vì thế, bất cứ đường nào nằm trên đường tròn cũng cách tâm O một khoảng đúng bằng bán kính. Vì thế, để chứng minh tứ giác nội tiếp đường tròn, cần chứng minh tất cả các điểm của tứ giác đều cách O một khoảng bằng R.
Ta có: Cho tứ giác ABCD và một điểm cố định O. Nếu học sinh có thể chứng minh được, các điểm A, B, C, D đều cách điểm O cho trước một khoảng bằng nhau là R. Nói cách khác, chứng minh được rằng, OA = OB = OC = OD = R thì tứ giác ABCD nội tiếp đường tròn tâm O bán kinh R.
Phương pháp 5: Chứng minh bằng phương pháp phản chứng
Theo lý thuyết, tất cả các hình tứ giác đặc biệt là hình vuông, hình chữ nhật, hình thoi hay hình bình hành đều là tứ giác nội tiếp của đường tròn tâm O.
Vì thế, để chứng minh một tứ giác ABCD bất kỳ là tứ giác nội tiếp đường tròn, học sinh có thể chứng minh tứ giác đó là tứ giác đặc biệt.
Như vậy, với 5 cách chứng minh trên đây, học sinh có thể dễ dàng chứng minh một tứ giác nội tiếp đường tròn bất kỳ, hoặc một hình tròn ngoại tiếp tứ giác. Tuy nhiên, học sinh cũng cần lưu ý những cách chứng minh trên để không nhầm lẫn giữa các phương pháp.
Có thể bạn quan tâm: Diện tích hình tròn là gì? Có những công thức nào để tính?
Một số lưu ý khi chứng minh tứ giác nội tiếp đường tròn
Để học sinh có thể dễ dàng chứng minh một tứ giác nội tiếp đường tròn hay không không chỉ phụ thuộc vào 5 phương pháp trên. Vì thế, người học cần nắm rõ một vài lưu ý dưới đây để có thể không bị mắc bẫy của người ra đề nhé.
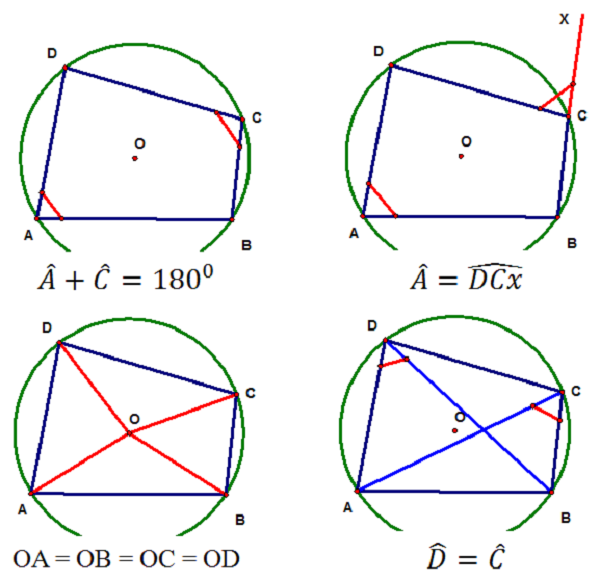
- Khi vẽ hình, học sinh nên vẽ các điểm rõ ràng và tránh vẽ tại các điểm thuộc trường hợp đặc biệt. Nếu đề bài chỉ yêu cầu cho tứ giác ABCD bất kỳ, người học không được vẽ thành các trường hợp đặc biệt như hình vuông, hình chữ nhật, hình thoi hay hình bình hành. Điều này có thể dẫn đến bài làm bị sai.
- Trong bài, các ký hiệu như góc, đoạn thẳng bằng nhau cần được ký hiệu rõ ràng để trong quá trình chứng minh không bị sai.
- Cần bám chắc vào các giả thiết, các lý thuyết và yêu cầu của đề thi để không lan man.
- Một số đề bài thường cho gợi ý rất rõ ràng, vì thế, những yêu cầu của đề bài có thể là thông tin quan trọng để chứng minh.
- Tránh không được dùng các điều đang cần chứng minh là điều hiển nhiên để chứng minh lại chúng.
Bài viết về các cách chứng minh đường tròn nội tiếp trên đây đã giúp học sinh, giáo viên và người nhà có thể hoàn thành bài tập một cách hiệu quả. Chúng tôi hy vọng rằng những phương pháp trên đây có thể giúp bạn có thêm những cách chứng minh nhanh chóng nhất.
Có thể bạn quan tâm: Tìm hiểu khái niệm, dấu hiệu nhận biết và cách tính diện tích hình bình hành
