Trong phần hình học của môn Toán bậc THPT thì rất đa dạng về các loại kiến thức, đặc biệt là hình học không gian. Điển hình như hình lập phương. Vậy hình lập phương là gì? Công thức tính chu vi, diện tích và thể tích hình lập phương như thế nào? Bài viết dưới đây sẽ chia sẻ chi tiết những kiến thức, các bài tập và một số kiến thức mở rộng hình lập phương để bạn có thể tham khảo và củng cố lại.
1. Hình lập phương là gì?

Hình lập phương là hình khối có chiều rộng, chiều dài và chiều cao đều bằng nhau.
Hình lập phương có:
• 8 đỉnh: đỉnh A, đỉnh C, đỉnh B, đỉnh D, đỉnh E, đỉnh F, đỉnh G, đỉnh H
• 12 cạnh bằng nhau: AB = BD = DC = CA = CH = AE = DG = BF = FG = FE = EH = HG
• Có 9 số mặt phẳng đối xứng
• Có 4 đường chéo cắt ngang tại một điểm, được xem là tâm đối xứng của hình lập phương.
• Đường chéo các mặt bên của khối lập phương đều dài bằng nhau
• Đường chéo của hình lập phương cũng dài bằng nhau.
• 6 mặt là hình vuông bằng nhau
2. Công thức tính diện tích hình lập phương
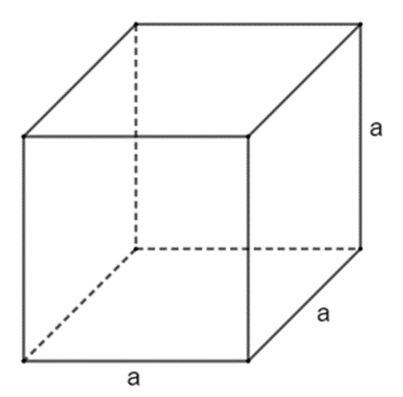
2.1. Diện tích xung quanh hình lập phương
Bằng diện tích một mặt nhân với 4.
Sxq = a . a . 4
2.2. Diện tích toàn phần hình lập phương
Bằng diện tích một mặt nhân với 6.
Stp = a . a . 6
3. Cách tính thể tích hình lập phương
Công thức tính thể tích hình lập phương ta lấy cạnh nhân với cạnh nhân rồi nhân với cạnh.
V = a . a . a
4. Công thức tính chu vi hình lập phương
P = 12 . a
5. Công thức tính đường chéo hình lập phương

Đường chéo của hình lập phương hợp với các đường cao tạo thành 1 tam giác vuông
Áp dụng định lý Py-ta-go, ta có công thức tính đường chéo D
Trong đó:
• D là độ dài đường chéo hình lập phương
• d là độ dài đường chéo 1 mặt
• a là độ dài cạnh hình lập phương
4. Cách vẽ hình lập phương
Vẽ hình lập phương ABCDEFGH:
• Bước 1: Vẽ mặt đáy: vẽ hình bình hành ABCD – chính là mặt đáy hình lập phương ABCDEFGH.
• Bước 2: Lần lượt dựng các đường cao có độ dài a, ta được các đường cao AE, BF, CG, DH = a.
• Bước 3: Nối các đỉnh E,F,G,H ta được hình lập phương ABCDEFGH
Lưu ý: Kẻ nét đứt cho AD, DC, FD vì đây là những đoạn bị lấp.
.jpg)
5. Bài tập liên quan đến hình lập phương
Bài 1: Tổng số mặt, số cạnh và số đỉnh của một hình lập phương là:
A. 26.
B. 25.
C. 24.
D. 23.
ĐÁP ÁN
∗ Phương pháp
Hình lập phương là hình có 6 mặt đều là các hình vuông.
∗ Cách giải
Hình lập phương có 6 mặt, 8 đỉnh và 12 cạnh nên tổng số cạnh, mặt đỉnh là: 6 + 8 + 12 = 26.
→ Chọn câu A.
Bài 2: Hình lập phương thuộc loại khối đa diện đều nào?
A. {5;3}.
B. {3;4}.
C. {4;3}.
D. {3;5}.
ĐÁP ÁN
∗ Phương pháp
Mỗi khối đa diện xác định bởi kí hiệu {p;q}, trong đó p là số các cạnh mỗi mặt ( hoặc số các đỉnh mỗi mặt) và q là số các mặt gặp nhau ở một đỉnh.
∗ Cách giải
Do hình lập phương là hình có 6 mặt và mỗi mặt có 4 đỉnh. Hơn nữa mỗi đỉnh là giao của ba mặt nên theo trên ta có p = 4; q = 3. Vậy hình lập phương là khối đa diện đều {4;3}.
→ Chọn câu C.
Bài 3: Cho hình lập phương ABCD.A’B’C’D’ có diện tích tam giác ACD’ bằng . Tính thể tích V của hình lập phương.
A. V = 8a3
B. V = a3
C. V =
D. V =
ĐÁP ÁN
∗ Phương pháp
Thể tích của hình lập phương cạnh a: V = a3
∗ Cách giải

Gọi cạnh của hình lập phương là x
Khi đó
Xét tam giác AA’D vuông tại A ta có:
Tương tự có:
⇒ AD’C là tam giác đều cạnh
⇒
⇔
⇒
→ Chọn câu C.
Bài 4: Hình lập phương ABCD.A’B’C’D’ cạnh a. Tính thể tích khối tứ diện ACB’D’.
A.
B.
C.
D.
ĐÁP ÁN
∗ Phương pháp
Công thức tính thể tích hình lập phương cạnh a: V = a3
∗ Cách giải

→ Chọn câu A.
Bài 5: Tính thể tích của hình lập phương có cạnh bằng 4.
A.
B. 64
C. 16
D. 4
ĐÁP ÁN
∗ Phương pháp
Thể tích của hình lập phương có cạnh bằng a là: V = a3
∗ Cách giải
Thể tích của hình lập phương có cạnh bằng 4 là: V = 43 = 64
→ Chọn câu B.
Thông qua lý thuyết và bài tập ở trên ta có thể thấy để đạt được điểm ở phần hình lập phương rất là dễ dàng, chúng ta cần phải nắm bắt và thuộc các lý thuyết một cách rõ ràng để có thể nhận biết, bên cạnh đó có thể giải quyết bài tập liên quan một cách nhanh chóng.
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang
