Trong chương trình toán học ở trung học phổ thông, hình học không gian là một trong những phần khó và khiến nhiều người lo lắng nhất. Đây cũng là phần xuất hiện trong đề thi đại học với số điểm khá lớn. Vậy, trong bài viết hôm nay chúng tôi sẽ nhắc lại một kiến thức trọng tâm về phần này. Đó là tứ diện đều. Cùng theo dõi nhé.
Khái niệm tứ diện đều
Tứ diện đều là một dạng tứ diện đặc biệt, được sử dụng cực kỳ nhiều trong các bài tập hình học không gian. Để định nghĩa chính xác về dạng hình này, chúng ta có thể sử dụng 3 cách như sau
- Là một hình chóp có đáy là tam giác đều ( hình chóp tam giác đều)
- Là một hình tứ diện có 4 mặt xung quanh là 4 hình tam giác đều
- Là một hình chóp tam giác đều với 3 cạnh bên có độ dài bằng 3 cạnh đáy
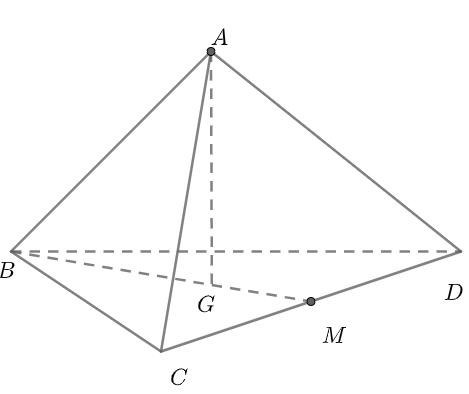
Để vẽ một tứ diện đều như hình trên, bạn có thể tiến hành theo các bước như sau:
Bước 1: Vẽ một hình tam giác đều làm mặt đáy hình chóp. Trong trường hợp này cụ thể là tam giác BCD
Bước 2: Trong tam giác BCD vừa vẽ xong, kẻ một đường trung tuyến xuất phát từ đỉnh B nối xuống trung điểm M của CD là BM
Bước 3: Trên đường trung tuyến BM, xác định trọng tâm G của tam giác sao cho BG = 2GM
Bước 4: Dựng đường cao của hình chóp xuất phát từ trọng tâm G đi lên. Chọn A làm đỉnh của hình chóp
Bước 5: Từ A nối các đường AB, AC, AD tạo thành 3 cạnh bên là xong
Vậy, một hình tứ diện đều A.BCD sẽ có lần lượt các thành phần như sau
- 4 đỉnh: A, B, C, D
- 6 cạnh: AB, AC, AD, BC, CD, BD
- 4 mặt: (ABC), (ACD), ( ABD), ( BCD)
Có thể bạn quan tâm: Thể tích hình trụ được tính như thế nào? Lưu ý gì khi tính thể tích hình trụ?
Những tính chất cơ bản của hình tứ diện đều
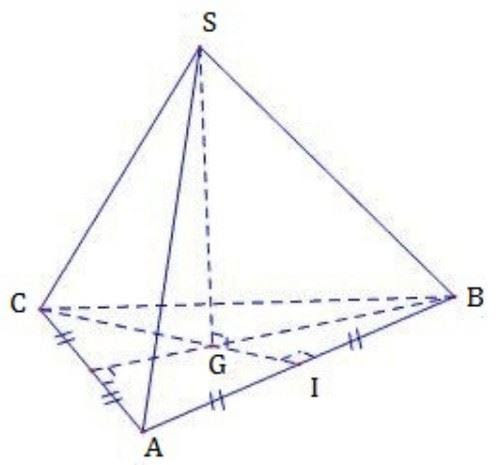
Cho hình tứ diện đều S.ABC như hình dưới đây, từ định nghĩa, ta có thể suy ra một số tính chất như sau
- 4 mặt bên của hình chóp là 4 tam giác bằng nhau:
 =
= 
- Tất cả các mặt xung quanh của hình chóp đều là những tam giác có góc nhọn:
- Tổng của 3 góc tại một đỉnh bất kỳ của hình chóp luôn là
- Hai cạnh bất kỳ trong tứ diện đối diện nhau đều có độ dài bằng nhau: CS=AB, SB=AC, SA=BC
- Tâm của tứ diện trùng với tâm của mặt cầu ngoại tiếp và nội tiếp hình chóp
- Hình hộp ngoại tiếp hình chóp S.ABC là hình hộp chữ nhật
- 3 trục đối xứng của hình chóp lần lượt là đường thẳng nối từ đỉnh đến tâm của mặt phẳng đối diện. 3 trục này có độ dài hoàn toàn bằng nhau
- Tổng cosin của các góc phẳng nhị diện trên cùng một mặt phẳng của hình chóp bằng 1
- Đoạn thẳng đi qua trung điểm của 2 cạnh đối diện nhau sẽ vuông góc với cả 2 cạnh
- Tất cả các góc phẳng nhị diện tương ứng với mỗi cặp cạnh đối diện nhau trong hình chóp đều có độ dài bằng nhau
Có thể bạn quan tâm: Tìm hiểu khái niệm, dấu hiệu nhận biết và cách tính diện tích hình bình hành
Một số công thức cơ bản và bài tập ví dụ
Với mỗi một khối tứ diện đều với 6 cạnh và 4 mặt bằng nhau, ta đều có thể sử dụng các công thức tính toán cơ bản như sau
- Thể tích: S =
- Chiều cao: h =
Ví dụ 1: Cho khối tứ diện đều ABCD. Tính thể tích của hình khi biết độ dài cạnh
- AB = 5cm
- BC = 3cm
- CD = 6cm
Cách giải:
- Vì ABCD là một hình chóp tam giác với 6 cạnh bằng nhau nên ta có AB=AC=AD=BC=BC=CD=5cm. Vậy thể tích cần tìm là
V = = 14,7
- Sử dụng công thức tương tự ta có
V =  = 3,2
= 3,2
V =  = 25,5
= 25,5
Ví dụ 2: Tính thể tích khối chóp tam giác đều cạnh 2x
Cách giải:
Áp dụng công thức tính thể tích, ta có công thức như sau
V = =
Ví dụ 3: Cho khối tứ diện đều ABCD có chiều cao bằng
Cách giải
Theo đề ta có: h =
Vậy, thể tích của ABCD là V =
Trên đây là bài viết tóm tắt một số kiến thức cơ bản về tứ diện đều mà chúng tôi muốn chia sẻ đến các bạn. Hy vọng những thông tin này sẽ giúp bạn ôn luyện một số kiến thức quan trọng cho bản thân mình. Và cũng đừng quên thường xuyên truy cập vào website của ReviewAZ hàng ngày để cập nhật những tin tức khác nhé
Có thể bạn quan tâm: Cách tính chu vi hình tròn và các bài tập ví dụ về tính chu vi hình tròn

 =
=