Các bạn đã hiểu rõ về diện tích hình lục giác đều hay chưa? Vậy các bạn hãy cùng mình tìm hiểu diện tích hình lục giác đều cùng Studytienganh.vn nhé!
1. Hình lục giác đều là gì?
Hình lục giác còn được gọi là hình sáu cạnh được xem là một đa giác, là một dạng hình thể trong hình học phẳng. Lục giác là hình bao gồm sáu góc và sáu cạnh.
Theo đó, lục giác đều là hình có 6 cạnh đều nhau và 6 cạnh này có cùng chiều dài. Để phân biệt, khi bạn thấy một hình lục giác có 6 cạnh và 5 góc bằng nhau thì đó là hình lục giác đều.
( Hình ảnh về hình lục giác đều)
Ngoài ra, một hình khối được cấu tạo bởi hai đáy hình lục giác được gọi là lục lăng.
Trong lý thuyết hình học, lục giác đều có các tính chất – đặc điểm như sau:
– Đa giác này có tổng cộng 6 hình tam giác đều. Bạn sẽ nhìn thấy 6 hình này bằng cách nối tâm đường tròn ngoại tiếp và nội tiếp với đỉnh của đa giác.
– Các cạnh trong hình 6 cạnh có độ dài bằng nhau và có các góc ở đỉnh bằng nhau.
– Tâm của đường tròn nội tiếp và đường tròn ngoại tiếp là tâm đối xứng quay.
– Chiều dài các cạnh của đa giác dài đúng bằng với bán kính của đường tròn ngoại tiếp.
– Các cạnh liền kề nhau trong đa giác đều tạo thành một góc 120 độ.
2. Cách tính diện tích
Muốn tính diện tích của hình lục giác thường, ta có thể chia hình lục giác thành 4 hình tam giác, tính tổng diện tích của các tam giác đó là tìm ra diện tích của hình lục giác.
Để tính được diện tích của hình lục giác đều, ta sử dụng công thức như sau:
S = 3√3 a2 : 2
Trong đó:
S là kí hiệu diện tích
a là độ dài cạnh của lục giác
a. Tính diện tích hình lục giác đều khi biết độ dài một cạnh
– Trường hợp đề bài cho sẵn độ dài một cạnh:
Đối với trường hợp này bạn chỉ cần thay số mà đề bài đã cho vào công thức tính diện tích.
– Trường hợp xác định độ dài qua chu vi (P):
Bạn sẽ thông qua công thức P = 6 x a => a = P : 6 để tìm cạnh của một hình lục giác đều bất kỳ. Sau khi xác định được chiều dài của cạnh bạn chỉ cần thay vào công thức tính diện tích.
Tính diện tích hình lục giác đều khi biết đường trung đoạn
Trung đoạn là đoạn thẳng vuông góc kẻ từ tâm của lục giác đều đến một cạnh bất kỳ của nó.
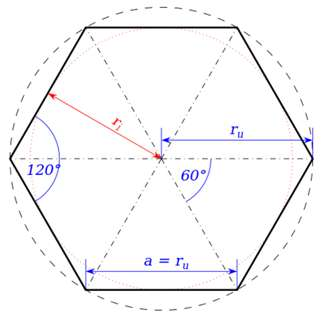
( Hình ảnh về các cách tính diện tích hình lục giác đều)
b. Tính diện tích hình lục giác không đều khi biết các đỉnh
– Bước 1: Xác định tọa độ các đỉnh của đa giác không đều.
Bạn hãy xác định tọa độ của tất cả các đỉnh lục giác bằng hệ trục tọa độ x, y. Khi biết tọa độ các đỉnh của một hình lục giác thì bạn sẽ dễ dàng tính được diện tích của nó.
– Bước 2: Tạo bảng giá trị tọa độ.
Bạn hãy lập một bảng liệt kê tọa độ x, y của mỗi đỉnh theo thứ tự ngược chiều kim đồng hồ và lặp lại giá trị đầu tiên ở cuối bảng.
– Bước 3: Tính nhóm kết quả (1)
Lấy tọa độ x của đỉnh trước nhân với giá trị y của đỉnh tiếp theo rồi cộng các tích lại với nhau.
– Bước 4: Tính nhóm kết quả hai (2)
Ngược với bước 3, tại bước này ta sẽ lấy tọa độ y của đỉnh trước nhân với tọa độ x của đỉnh tiếp theo rồi lấy tổng các tích.
– Bước 5: Lấy tổng các tích của nhóm (1) trừ đi tổng các tích của nhóm (2) sau đó lấy trị tuyệt đối của kết quả.
– Bước 6: Tính diện tích của lục giác không đều.
Thương của kết quả ở bước năm chia cho hai sẽ là diện tích của lục giác không đều.
c. Cách tính chu vi
Các bạn học sinh chỉ cần áp dụng công thức tính chu vi hình lục giác đều là P = 6 x a => suy ra tìm a bằng công thức
a = P : 6
để tìm cạnh của một hình lục giác đều bất kỳ.
Trong đó:
S là kí hiệu chu vi
a là độ dài cạnh của lục giác.
Tính bán kính đường tròn ngoại tiếp của hình lục giác đều
Công thức bán kính tính đường tròn ngoại tiếp của hình lục giác đều : R = a
Trong đó:
R là bán kính đường tròn ngoại tiếp
a là độ dài cạnh của lục giác.
Tính bán kính đường tròn nội tiếp của hình lục giác đều
Công thức tính bán kính đường tròn ngoại tiếp của hình lục giác đều :
r = a√32
Trong đó:
r là bán kính đường tròn nội tiếp
a là độ dài cạnh của lục giác.
3. Bài tập minh họa
Bài tập 1: Tìm diện tích và chu vi của hình lục giác, nếu tất cả các cạnh của nó có độ dài bằng 6cm.
Đáp án bài tập 1:
Ta có độ dài cạnh a của lục giác đều bằng 6cm, nên áp dụng công thức phía trên:
S = 2,59807 a2 = 2,59807.62 = 93,53 cm2
Chu vi hình lục giác đều
P = 6.a = 6.6 = 36cm.
Bài tập 2: Tìm cạnh của lục giác đều nếu chu vi của nó bằng 48cm
Đáp án bài tập 2:
Ta có được chu vi lục giác đều là 48cm nên => p = 6a < = > 48 = 6.a
Trên đây là những kiến thức về diện tích hình lục giác đều mà các bạn có thể tham khảo. Chúc các bạn có những kiến thức bổ ích cùng Studytienganh.vn
